线性代数(经管类)2011年10月真题试题及答案解析(04184)
部分试题预览
-
设A是3阶反对称矩阵,证明|A|=0.
-
用配方法化二次型
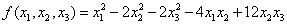 为标准形,并写出所作的可逆线性变换.
为标准形,并写出所作的可逆线性变换. -
已知2阶方阵A的特征值为
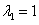 及
及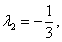 方阵B=A2
方阵B=A2(1)求B的特征值;
(2)求B的行列式.
-
设向量组α1=(1,1,1,3)T,α2=(-1,-3,5,1)T,α3=(3,2,-1,p+2)T,α4=(3,2,-1,p+2)T问p为何值时,该向量组线性相关?并在此时求出它的秩和一个极大无关组.
-
设3元线性方程组
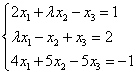 ,
,(1)确定当λ取何值时,方程组有惟一解、无解、有无穷多解?
(2)当方程组有无穷多解时,求出该方程组的通解(要求用其一个特解和导出组的基础解系表示).
-
解矩阵方程

-
设矩阵
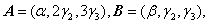 其中
其中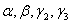 均为3维列向量,且
均为3维列向量,且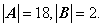 求
求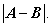
-
设矩阵
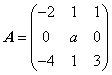 有一个特征值λ=2对应的特征向量为
有一个特征值λ=2对应的特征向量为 则数a=____
则数a=____ -
设实二次型
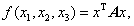 已知A的特征值为-1,1,2,则该二次型的规范形为.
已知A的特征值为-1,1,2,则该二次型的规范形为. -
设3阶方阵A的秩为2,且
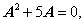 则A的全部特征值为__
则A的全部特征值为__
相关试卷
2019年4月外刊经贸知识选读真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2008年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2009年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2009年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2010年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2010年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2011年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2011年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2012年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2012年7月真题试
所属类型:真题考试2021-03-24
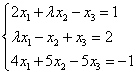 ,
,
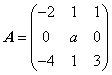 有一个特征值λ=2对应的特征向量为
有一个特征值λ=2对应的特征向量为 则数a=____
则数a=____