高职单招考试数学考前押题试卷附答案（五）

如图所示，四棱锥中P-ABCD，底面ABCD为矩形，点E为PB的中点.

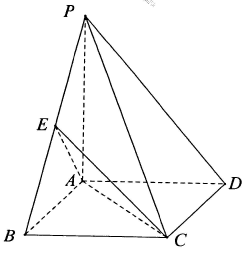
求证：PD//平面ACE.

己知椭圆与抛物线y²=4x有共同的焦点F₂，过椭圆的左焦点F₁作倾斜角为的直线，与椭圆相交于M、N两点.求：

(1) 直线MN的方程和椭圆的方程;

(2) △OMN的面积.

甲、乙两人进行投篮训练，己知甲投球命中的概率是1/2，乙投球命中的概率是3/5,且两人投球命中与否相互之间没有影响.

(1) 若两人各投球1次，求恰有1人命中的概率;

(2) 若两人各投球2次，求这4次投球中至少有1次命中的概率.

设函数f(x)既是R上的减函数，也是R上的奇函数，且f(1)=2.

(1) 求f(-1)的值;

(2) 若f(t²-3t+1)>-2，求t的取值范围.

若 f(X) =，则f(2)=     。

己知{a_n}为等差数列，其前n项和为S_n，若a₃=6, S₃= 12,求公差d.

设A(2,-4), B(0,4),则线段AB的中点坐标为     。

若△ABC 中，∠C=90°,|AC|=3,|BC|=4,则=     。

(x+2)⁶的展开式中x³的系数为     。