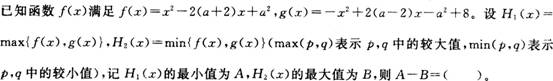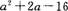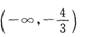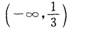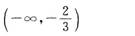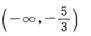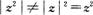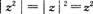2014年教师资格考试《中学数学学科知识与教学能力》模拟卷(3)
-
请以“定义与命题”为课题,完成下列教学设计。要求:写出较为完整的教学设计方案。
-
谈谈你对数学新课程所提倡的评价方式与方法的认识。
-
根据下面案例,请你谈谈自己对提问的看法,并设计几个提问。一堂讲菱形的判定定理(是讲对角线互相垂直平分的四边形是菱形)的课,教师画出图形后,有一段对话:师:四边形ABCD中,AC与BD互相垂直平分吗?生:是!师:你怎么知道?生:这是已知条件!师:那么四边形ABCD是菱形吗?生:是的!师:能通过证三角形全等来证明结论吗?生:能!
-

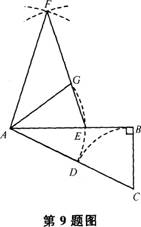
(1)求AE的长度;
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由。
-
你认为一堂好课的特点应体现在哪些方面?
-

-
某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组。在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占l0%。登山组的职工
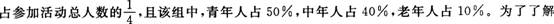
各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体
职工中抽取一个容量为200的样本,试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数。
-
简述两条以上传统的学生数学学习评价中存在的主要问题。
-
已知二次函数y=ax2+bx+c(a≠0)的图像如图,则下列结论中正确的是( )。
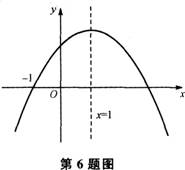
- A.a>;0
- B.当x>;1时,y随x的增大而增大
- C.c<;O
- D.3是方程ax2+bx+c=0的一个根
-
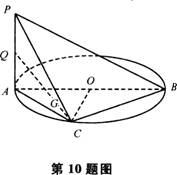
如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆O上的点。(1)求证:BC⊥平面PAC;(2)若Q为PA的中点,G为△AOC的重心,求证:QG//平面PBC。
-
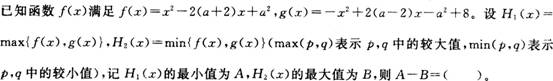
- A.

- B.
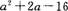
- C.
-16
- D.
16
- A.A
- B.B
- C.C
- D.D
- A.
-

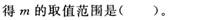
- A.
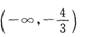
- B.
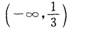
- C.
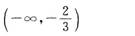
- D.
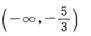
- A.A
- B.B
- C.C
- D.D
- A.
-
如图,海边有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是(⊙O的一部分)区域内,∠AOB=80°,为了避免触礁,轮船P与A、B的张角∠APB的最大值为( )。
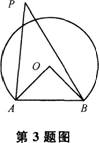
- A.20°
- B.30°
- C.40°
- D.60°
-
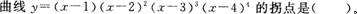
- A.(1,0)
- B.(2,0)
- C.(3,0)
- D.(4,0)
-
已知a,b为两条不同的直线,α,β为两个不同的平面,且a⊥α,b⊥β,则下列命题中的假命题是( )。
- A.若a//b,则α∥β
- B.若α⊥β,则a⊥b
- C.若a,b相交,则α,β相交
- D.若α,β相交,则a,b相交
-
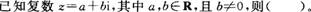
- A.
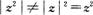
- B.
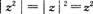
- C.
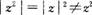
- D.
- A.A
- B.B
- C.C
- D.D
- A.
-
- A.
- B.
- C.
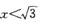
- D.
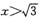
- A.A
- B.B
- C.C
- D.D
- A.