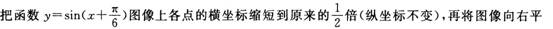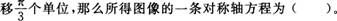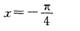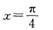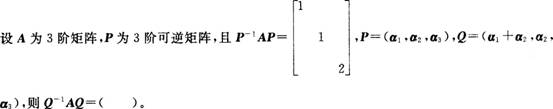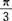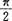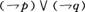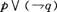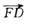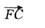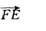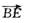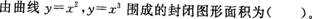2014年教师资格考试《中学数学学科知识与教学能力》专家预测试卷(1)
-
请以“分式方程(1)”为课题,完成下列教学设计。(1)教学目标;(2)教学重点、难点;(3)教学过程(要求写出新课导入和新知探究、巩固、应用等)。
-
材料:下面是一堂有关“平行线及其性质”的教学过程:
(一)创设情境,设疑激思
1.播放一组幻灯片,内容:①供火车行驶的铁轨;②游泳池中的泳道隔栏;③横格纸中的线。
2.提问温故:日常生活中我们经常会遇到平行线,你能说出直线平行的条件吗?
3.学生活动:针对问题,学生思考后回答——①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行;
4.教师肯定学生的回答并提出新问题:若两直线平行,那么同位角、内错角、同旁内角各有什么关系呢?从而引出课题:探索平行线的性质(板书)
(二)数形结合。探究性质
1.画图探究,归纳猜想
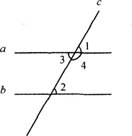
教师提要求,学生实践操作:任意画出两条平行线(a∥b),画一条截线c与这两条平行线相交,标出8个角。(统一采用阿拉伯数字标角)
教师提出研究性问题一:
指出图中的同位角,并度量这些角,把结果填入下表:
教师提出研究性问题二:
将图中的同位角任意一组剪下后叠合。

让学生根据活动的数据与操作得出的结果归纳猜想:两直线平行,同位角相等。
教师提出研究性问题三:
再画出一条截线d,看你的猜想结论是否仍然成立?
学生活动:探究,按小组讨论,最后得出结论:仍然成立。
2.教师用《几何画板》课件验证猜想,让学生直观感受猜想。
3.教师展示平行线性质(1):两条平行线被第三条直线所截,同位角相等。(两直线平行,同位角相等)
(三)引申思考,培养创新
教师提出研究性问题四:请判断两条平行线被第三条直线所截,内错角、同旁内角各有什么关系?
学生活动:独立探究一——小组讨论——成果展示。
教师活动:评价学生的研究成果,并引导学生说理。
因为a∥b(已知),
所以∠1=∠2(两直线平行,同位角相等)。
又∠1=∠3(对顶角相等),
∠1+∠4=180°(邻补角的定义),
所以∠2=∠3(等量代换),
∠2+∠4=180°(等量代换)。
教师展示:
平行线性质(2):两条平行线被第三条直线所截,内错角相等。(两直线平行,内错角相等)
平行线性质(3):两条平行线被第三条直线所截,同旁内角互补。(两直线乎行,同旁内角互补)
(四)实际应用。优势互补
1.(抢答)课本P13练一练1、2及习题7.2 1、5
2.(讨论解答)课本P13习题7.22、3、4;
(五)课堂总结
这节课你有哪些收获?
1.学生总结:平行线的性质1、2、3
2.教师补充总结:
(1)用“运动”的观点观察数学问题;(如我们前面将同位角剪下叠合后分析问题)
(2)用数形结合的方法来解决问题;(如我们前面将同位角测量后分析问题)
(3)用准确的语言来表达问题;(如平行线的性质1、2、3的表述)
(4)用逻辑推理的形式来论证问题。(如我们前面对性质2和3的说理过程)
(六)作业
学习与评价P51、2、3(填空);
4、5、6(选择);
7、8(拓展与延伸)
16.与传统课堂教学相比,该堂课的设计有哪些变化?
-
谈谈如何促进解题方式的多样化。
-

-
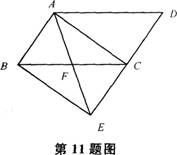
如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F。

-

-

(1)要使生产该产品2小时获得的利润不低于3000元,求x值的取值范围;
(2)要使生产900千克该产品获得的利润最大,问甲厂应该选取何种生产速度?并求此最大利润。
-
简述《课标》中总体目标四个方面的关系。
-
学生的数感主要表现在哪些方面?
-
- A.

- B.
- C.

- D.
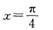
- A.A
- B.B
- C.C
- D.D
- A.
-
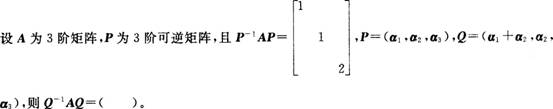
- A.
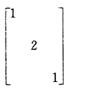
- B.
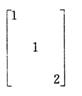
- C.

- D.

- A.A
- B.B
- C.C
- D.D
- A.
-
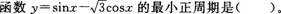
- A.
π
- B.
2π
- C.
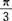
- D.
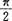
- A.A
- B.B
- C.C
- D.D
- A.
-
在一次跳伞训练中,甲、乙两位学员各跳一次,设命题P是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“至少有一位学员没有降落在指定范围”可表示为( )。
- A.
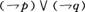
- B.
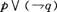
- C.

- D.
P ∨ q
- A.A
- B.B
- C.C
- D.D
- A.
-
下列命题是真命题的是( )。
- A.无限小数是无理数
- B.相反数等于它本身的数是0和1
- C.对角线互相平分且相等的四边形是矩形
- D.等边三角形既是中心对称图形,又是轴对称图形
-

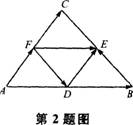
- A.
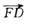
- B.
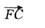
- C.
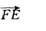
- D.
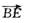
- A.A
- B.B
- C.C
- D.D
- A.
-
用导数的定义求函数f(x)=2x+3在指定点f‘(0)的值是( )。
- A.1
- B.2
- C.3
- D.0
-
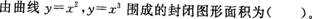
- A.1/12
- B.1/4
- C.1/3
- D.7/12