全国2014年10月高等教育自学考试《高等数学基础》试题
-
由直线y=2-x,x轴和抛物线y=x2(x>0)所围的图形为D,求(1)D的面试S(2)D绕x轴旋转所得旋转体的体积V.
-
做一个底为圆,容积为125π立方米的圆柱形开口容器,怎样做法用料最省?
-
用基础解系表示齐次线性方程组
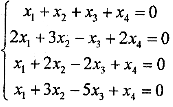 的全部解.
的全部解. -
求直线l:
 与平面π:2x+y-z-3=0的焦点及交角的正弦.
与平面π:2x+y-z-3=0的焦点及交角的正弦. -
求定积分

-
已知y=ln(1+ex),求y''
-
已知矩阵
 ,求A的秩.
,求A的秩. -
求函数y=xarctanx-
 的微分dy
的微分dy -
求极限

-
求不定积分ln(1+x2)dx
-

-
设A是m×n矩阵,其秩为5,则Ax=0的基础解系中所含向量的个数是
-
曲线y=x3,x=1,y=0所围图形的面积为
-
不定积分

-
曲线f(x)=x3+ax2+bx+a2的拐点个数是
-
过点(2,1,1)且垂直于向量i+2j+k的平面方程为
-
函数y=3(x-1)2的单调增区间是
-
设A为n阶方阵,若有矩阵关系.AB=AC,则必有
- A.A=0
- B.B≠C时,A=0
- C.A≠0时,B=C
- D.︱A︱≠0时,B=C
-
若两向量
 =(λ,-3,2)和
=(λ,-3,2)和 =(1,2,-λ) 互相垂直,则λ=
=(1,2,-λ) 互相垂直,则λ= -

- A.0
- B.-1
- C.1
- D.2
-
定积分
 等于
等于- A.

- B.

- C.

- D.

- A.
-
函数f(x)=
 满足拉格朗日中值定理条件的区间是
满足拉格朗日中值定理条件的区间是- A.[-1,1]
- B.[-2,0]
- C.[0,1]
- D.[1,2]
-
已知∫f(x)dx=lnx+c,则f'(x)等于
- A.

- B.

- C.

- D.lnx
- A.
-
若函数f(x)=cosx+a2,其中a是常数,则f'(x)等于
- A.sinx+2a
- B.cosx+2a
- C.cosx
- D.-sinx
-
若f(x)在x=x0处可导,且f(x0)=0则
 等于
等于- A.f'(x)
- B.f'(x0)
- C.∞
- D.不存在
-

- A.∞
- B.0
- C.1
- D.不存在
-

- A.以0为极限
- B.以1为极限
- C.

- D.不存在极限
-
在空间直角坐标系下,方程3y+2z=0的图形表示为
- A.通过x轴的平面
- B.垂直于X轴的直线
- C.垂直于X轴的平面
- D.通过原点的直线
-
下列各点在第V卦限的点是
- A.(2,一3,4)
- B.(2,3,-4)
- C.(2,-3,-4)
- D.(-2,-3,4)
-

- A.

- B.
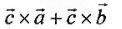
- C.

- D.

- A.
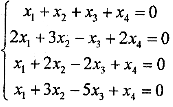 的全部解.
的全部解. ,求A的秩.
,求A的秩.


 等于
等于