数量方法(二)2014年10月全国统一真题题试卷（00994）
-
某地区居民l983--1987年人均收入与商品的销售额数据如题33表所示：
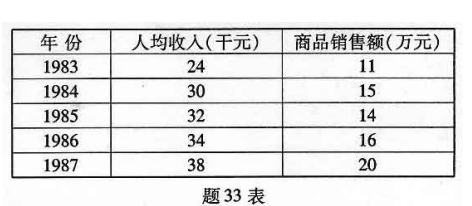
要求：(1)计算人均收入与商品销售额之间的简单相关系数;(3分)
(2)以商品销售额为因变量，人均收人为自变量，建立线性回归方程;(5分)
(3)计算估计标准误差。(2分)
-
生产商采用A、B两种新的生产工艺生产同种类型的产品。从使用工艺A和工艺B生 产的产品中分别随机抽取了l00件，测得它们的次品分别为6件和10件。
(1)求使用工艺A和工艺B生产的产品的样本次品率。(4分)
(2)能否认为使用工艺A生产的产品的次品率显著低于使用工艺B生产的产品的次品率(可靠性取95%)?请给出相应假设检验的原假设和备择假设。(6分)
-
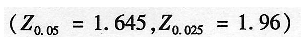
某地区国民生产总值(GNP)在l988-1989年平均每年递增5%，1990-1992年
平均每年递增2%，1993—1997年平均每年递增9%，试计算：
(1)该地区国民生产总值1988—1997这十年间的平均发展速度及平均增长速度;
(2)若1997年的国民生产总值为500亿元，以后每年增长8%，到2000年可达到多少亿?
-
某企业三种产品的生产情况如题31表所示：
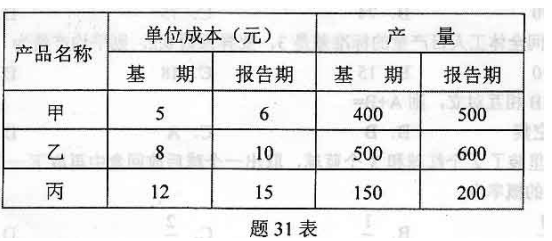
要求：(1)计算三种产品总成本指数;
(2)以报告期产量为权数计算单位成本指数。
-
从某饮料生产商生产的某种瓶装饮料中随机抽取l00瓶，测得其营养成分A含量的平均值为6.5克，样本标准差为l.0克。求该瓶装饮料中营养成分A含量的均值μ的 置信水平为95%的置信区间。
-
-
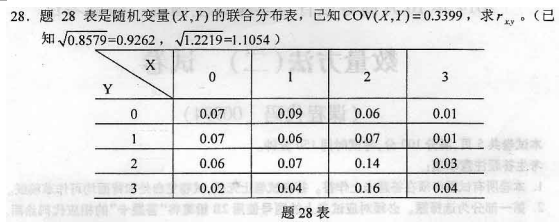
某集团下属20个企业去年利润数据如题26表1所示(单位：百万元)
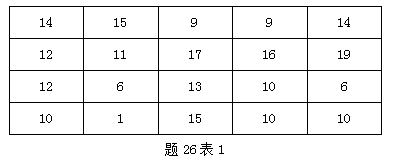
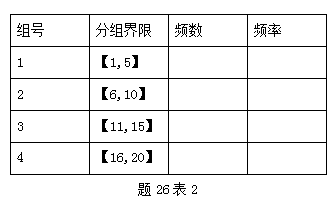
请按照题26表2给出的分组界限进行分组，并按照题26表2给出的格式完成频率分布表。
-
实战演习中，在甲、乙、丙三处射击的概率分别为0.2，O.7，0.1，而在甲、乙、丙三处射击时命中目标的概率分别为0.05，O.15，0.3。求演习中一次射击目标被击中的概率。
-
按月平均法计算的季节指数之和等于________。
-
在假设检验中，若犯第二类错误的概率增加，则显著性水平将________。
-
测量两变量之间线性关系密切程度的量是________。
-
假设总体参数
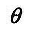的估计量为
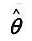，估计量的方差为D(
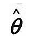)，偏差为b=E(
)-
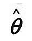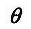，则估计量的均方误差
=________。 -
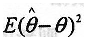在《数量方法》的一次考试中，一个学习小组8个同学的成绩分别是75、78、80、 85、86、88、88、88，则这8个同学考试成绩的中位数是________。
-
若价格持平，而贸易额增加，则贸易量指数
- A.下降
- B.不变
- C.上升
- D.不能确定
-
同一数量货币，报告期只能购买基期商品量的90%，这是因为物价上涨
- A.1.l0%
- B.0
- C.10%
- D.11.1%
-
已知某时间数列各期的环比增长速度分别为11%，13%，16%，该数列的定基发展速 度为
- A.11%×13%×16%
- B.111%×113%×116%
- C.(11%×13%×16%)-1
- D.(111%×113%×116%)-1
-
与回归估计标准误差的计量单位相同的是
- A.自变量
- B.因变量
- C.相关系数
- D.回归系数
-
对方差已知的正态总体均值的假设检验，可采用的方法为
- A.Z检验
- B.t检验
- C.F检验
- D.X2检验
-
检验总体是否服从正态分布，可以采用的统计检验方法是
- A.t检验
- B.Z检验
- C.F检验
- D.X2检验
-
如果相关系数r=1，则表明两个变量之间存在着
- A.正相关
- B.完全正相关
- C.完全负相关
- D.不相关
-
在大样本情况下，如果总体方差未知，利用正态分布构造的总体均值的置信区间为
- A.A
- B.B
- C.C
- D.D
-
在保持样本容量和抽样方式不变的情况下，若要缩小置信区间，则置信度会
- A.变大
- B.不变
- C.变小
- D.可能变小也可能变大
-
已知样本均值为
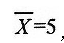，若将所有样本观察值都乘以1/5，则新的样本均值为- A.1
- B.2
- C.3
- D.4
-
计算估计标准误差的依据是
- A.总体的期望值
- B.总体的方差
- C.样本数据
- D.样本的均值
-
设随机变量X的分布律为P(X=K)=
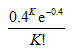, K=0,1，…则X的方差D(X)=- A.0.4
- B.2
- C.2.5
- D.25
-
已知某批水果的坏果率服从正态分布N(0.04，0.09)，则这批水果的坏果率的标准差为
- A.0.O4
- B.O.O9
- C.0.2
- D.0.3
-
设随机变量x的概率密度函数为
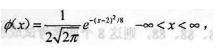则x的方差D(X)=- A.1
- B.2
- C.3
- D.4
-
事件A 、B 相互独立，P(A)=0.3，P(B|
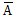)=0.6,则P(A)+P(B)=- A.0
- B.0.3
- C.0.9
- D.1
-
对任意两个事件A . B ,有
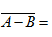
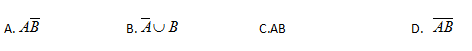
- A.A
- B.B
- C.C
- D.D
-
盒子里装了2个红球和3个蓝球，取出一个球后放回盒中再取下一个球。第二次取出 红球的概率为
- A.1/5
- B.1/2
- C.2/5
- D.1/3
-
A与B相互对立，则A+B=
- A.空集
- B.B
- C.A
- D.全集
-
某车间全体工人日产量的标准差是3，变异系数0.2，则平均产量为
- A.10
- B.15
- C.18
- D.20
-
某车间有2个生产小组负责生产某种零件，甲组有30名工人，乙组有20名工人。在 今年6月份，乙组平均每人生产80个零件，该车间50名工人平均每人生产74个零件，则甲组平均每人生产的零件数是
- A.70
- B.74
- C.75
- D.80
的估计量为
，估计量的方差为D(
)，偏差为b=E(
)-
，则估计量的均方误差
=________。
，若将所有样本观察值都乘以1/5，则新的样本均值为
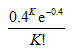, K=0,1，…则X的方差D(X)=
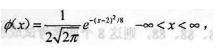则x的方差D(X)=
)=0.6,则P(A)+P(B)=
