数量方法(二)2014年4月全国统一真题题试卷（00994）

对某市的百货商店进行抽样调查，5家被抽查的商店职工月平均销售额和利润率数

要求：

(1)计算人均月销售额与利润率之间的简单相关系数;(3分)

(2)以利润率为因变量，人均月销售额为自变量，建立线性回归方程;(5分)

(3)计算估计标准误差。(2分)

某农场种植的苹果优等品率为40%，为提高苹果的优等品率，该农场采用了一种新的种植技术，采用后对于500个苹果组成的随机样本的测试表明，其中有300个苹果为优等品。

(1)求该农场种植苹果的样本优等品率。(2分)

(2)该农场种植苹果的优等品率是否有显著提高(可靠性取95%)并说明理由?请给出相应假设检验的原假设和备择假设。(8分)

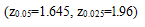
假设某单位员工每天用于阅读书籍的时间服从正态分布，现从该单位随机抽取了16名员工，己知他们用于阅读书籍的平均时间为50分钟，样本标准差为20分钟，试以95%的置信度估计该单位员工用于阅读书籍的平均时间的置信区间。

(已知t0.025(15)=2.13, t0.025(16)=2.12，t0.05(15)=1.753, t0.05(16)=1.746)

某煤矿2005年煤炭产量为25万吨，“十一五”期间(2006-2010)每年平均增长4%，以后每年平均增长5%，问到2015年该煤矿的煤碳产量将达到什么水平?

设某企业两种商品的销售额及销售量增长速度资料如题31表所示：

要求：(1)计算销售额指数;

(2)以基期销售额为权数计算销售量指数。

灯管厂生产出一批灯管，拿出5箱给收货方抽检。这5箱灯管被收货方抽检到的概率分别为0.2，0.3，0.1，0.1，0.3。其中，第一箱的次品率为0.02，第二箱的次品率为0，第三箱的次品率为0.03，第四箱的次品率为0.01，第五箱的次品率为0.01。收货方从所有灯管中任取一只，问抽得次品的概率是多少?

某型号零件的寿命服从均值为1200小时，标准差为250小时的正态分布。随机抽取一个零件，求它的寿命不低于1300小时的概率。

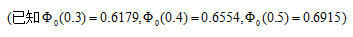
某企业2002年9月～12月月末职工人数资料如下：

则该企业第四季度的平均职工人数为________。

某车间牛产某种零件，20名工人日产零件数如颢26表1所示。

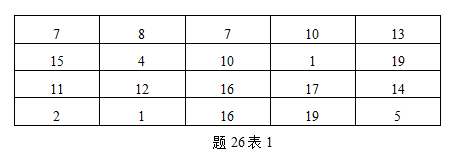
请按照题26表2给出的分组界限进行分组，并制作频率分布表。

对单个正态总体均值是否等于μ₀的检验，若方差σ²己知，样本容量为n，样本均值为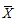，则检验统计量为________。

两个变量之间相关系数等于零，说明它们之间不存在________。

在点估计的基础上给出一个范围，使总体参数包括在这个范围内，推断总体参数有多大的概率被涵盖在这一范围内的参数估计方法称为________。

某种产品报告期与基期比较产量增长30%，单位成本下降35%，则生产费用支出总额为基期的

• A.84.5%
• B.90%
• C.175.5%
• D.184.5%

按照被描述的对象与时间的关系，数据可以分为截面数据、时间序列数据和________。

物价上涨后，同样多的人民币只能购买原有商品的96%，则物价上涨了

• A.4.17%
• B.4.5%
• C.5.1%
• D.8%

若己知时间数列的项数n，最初水平a0和平均增长量△，则可以求出

• A.各期发展水平
• B.各期发展速度
• C.各期的增长量
• D.平均增长速度

对于回归方程Y=a+bx，当b<0时，表示X与Y之间

• A.存在同方向变动关系
• B.存在反方向变动关系
• C.存在非线性关系
• D.不相关

若各观测点全部落在回归直线上，则

• A.估计标准误差S_y=1
• B.判定系数r²=0
• C.回归系数b=0
• D.剩余平方和SSE=0

当两个正态总体的方差己知时，欲比较两个正态总体均值的大小，可采用的检验方法为

• A.F检验
• B.t检验
• C.Z检验
• D.x²检验

设X₁，X₂，…，X_n为来自总体X~N(0,σ²)的样本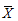，和S2分别为样本均值和样本方差，则统计量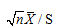服从的分布为

• A.N (0,1)
• B.x2(n-1)
• C.t (n-1)
• D.F (n,n-1)

在其他条件不变的情况下，若增大置信区间，则相应的置信概率

• A.将变小
• B.将变大
• C.保持不变
• D.可能变大也可能变小

在抽样推断中，样本的容量

• A.越少越好
• B.越多越好
• C.取决于统一的抽样比例
• D.取决于对抽样推断可靠性的要求

设Xl,X2，…，X50为来自正态总体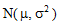的样本，则服从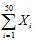

• A.A
• B.B
• C.C
• D.D

设随机变量X服从二项分布B (20,0.6)，则X的方差DX为

• A.3.6
• B.4.8
• C.6.0
• D.7.2

设总体X~U(μ₂,σ²)，则P(X＞μ)

• A.<1/4
• B.=1/4
• C.=1/2
• D.>1/2

将各种方案的最坏结果进行比较，从中选出收益最大的方案，此选择准则称为

• A.极小极大原则
• B.极大极小原则
• C.极小原则
• D.极大原则

事件A、B相互对立，P(A)=0.3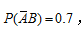则P(AB)=

• A.0
• B.0.3
• C.0.4
• D.1

某夫妇按照国家规定，可以生两胎。如果他们每胎只生一个孩子，则他们有一个男孩和一个女孩的概率为

• A.1/2
• B.1/4
• C.1/8
• D.1/16

设A、B、C为任意三个事件，则“这三个事件都发生”可表示为

• A.A
• B.B
• C.C
• D.D

对于峰值偏向右边的单峰非对称直方图，一般来说

• A.平均数>中位数>众数
• B.平均数<中位数<众数
• C.平均数>众数>中位数
• D.平均数<众数<中位数

将一枚硬币抛掷两次的样本空间Ω={00，01，10,11}(用0表示出现正面，用1表示出现反面)。“第一次出现正面”可以表示为

• A.{01,11}
• B.{10,11}
• C.{00,01}
• D.{00,11}

在一次《数量方法》考试中，某班的平均成绩是80分，标准差是4分，则该班考试成绩的变异系数是

• A.0.05
• B.0.2
• C.5
• D.20