设总体X~U(μ₂,σ²)，则P(X＞μ)

对某市的百货商店进行抽样调查，5家被抽查的商店职工月平均销售额和利润率数

要求：

(1)计算人均月销售额与利润率之间的简单相关系数;(3分)

(2)以利润率为因变量，人均月销售额为自变量，建立线性回归方程;(5分)

(3)计算估计标准误差。(2分)

某农场种植的苹果优等品率为40%，为提高苹果的优等品率，该农场采用了一种新的种植技术，采用后对于500个苹果组成的随机样本的测试表明，其中有300个苹果为优等品。

(1)求该农场种植苹果的样本优等品率。(2分)

(2)该农场种植苹果的优等品率是否有显著提高(可靠性取95%)并说明理由?请给出相应假设检验的原假设和备择假设。(8分)

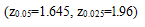
假设某单位员工每天用于阅读书籍的时间服从正态分布，现从该单位随机抽取了16名员工，己知他们用于阅读书籍的平均时间为50分钟，样本标准差为20分钟，试以95%的置信度估计该单位员工用于阅读书籍的平均时间的置信区间。

(已知t0.025(15)=2.13, t0.025(16)=2.12，t0.05(15)=1.753, t0.05(16)=1.746)

某煤矿2005年煤炭产量为25万吨，“十一五”期间(2006-2010)每年平均增长4%，以后每年平均增长5%，问到2015年该煤矿的煤碳产量将达到什么水平?

设某企业两种商品的销售额及销售量增长速度资料如题31表所示：

要求：(1)计算销售额指数;

(2)以基期销售额为权数计算销售量指数。

灯管厂生产出一批灯管，拿出5箱给收货方抽检。这5箱灯管被收货方抽检到的概率分别为0.2，0.3，0.1，0.1，0.3。其中，第一箱的次品率为0.02，第二箱的次品率为0，第三箱的次品率为0.03，第四箱的次品率为0.01，第五箱的次品率为0.01。收货方从所有灯管中任取一只，问抽得次品的概率是多少?

某型号零件的寿命服从均值为1200小时，标准差为250小时的正态分布。随机抽取一个零件，求它的寿命不低于1300小时的概率。

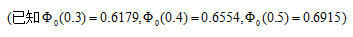
某企业2002年9月～12月月末职工人数资料如下：

则该企业第四季度的平均职工人数为________。

某车间牛产某种零件，20名工人日产零件数如颢26表1所示。

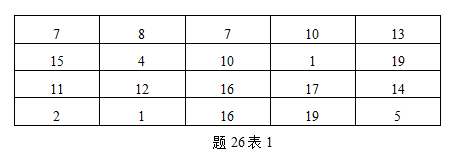
请按照题26表2给出的分组界限进行分组，并制作频率分布表。

对单个正态总体均值是否等于μ₀的检验，若方差σ²己知，样本容量为n，样本均值为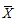，则检验统计量为________。