数量方法(二)2015年10月全国统一真题题试卷(00994)
-
在其它条件不变的情况下,某种商品的销售量(y)与该商品的价格(x)有关。现对给定时期内的价格与销售量进行观察,得到如题33表所示的一组数据:

现规定选用双曲线函数:
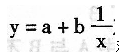 对价格与销售量进行回归分析。
对价格与销售量进行回归分析。要求:(1)以商品的销售量为因变量建立曲线回归方程;(8分)
(2) 当价格为8元时估计平均销售量。(2分)
-
已知某集市三种商品有关资料如题31表所示:
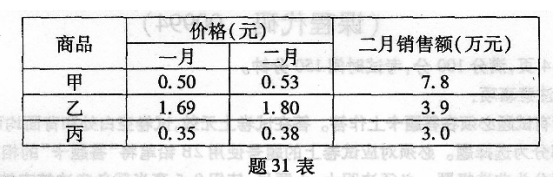
请以二月销售额为权数计算价格指数。
-
某厂家声称其生产的A品牌液晶显示器寿命不低于5万小时。从该厂家生产的一批A品牌液晶显示器中随机抽取9台,测得寿命分别为4.5,5,4.7,4.8,5.1,4.9,4.7,5,4.5(单位:万小时)。设该厂家生产的A品牌液晶显示器寿命服从正态分布。
(1)求该厂家生产的A品牌液晶显示器寿命的样本均值。(2分)
(2)求该厂家生产的A品牌液晶显示器寿命的样本方差。(2分)
(3)请以95%的可靠程度检验该厂家声明是否真实可信?并给出相应的原假设、备择假设及检验统计量。(6分)
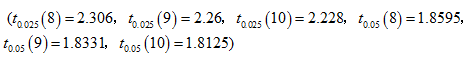
-
某企业历年来的工、世总产值资料如题30表所示:
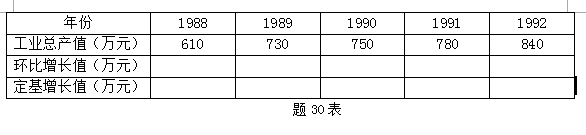
试计算该企业几年来的环比增长量、定基(以1988年为基期)增长量和年平均增长量。
请将题30表绘制在答题卡上作答。
-
某人估计其家庭九月份的电费(元)由下式决定:X=28.5+0.6C,其中C是九月份温 度,它是均值为34.2、标准差为2.2的连续型随机变量。求该家庭九月份的平均电费以 及电费的标准差。
-
假设由某汽车制造商提供的36辆新车组成的样本中,每辆新车的疵点数如下:1 2 0 0 3 0 1 1 2 2 2 0 1 0 2 0 1 3 0 1 2 1 0 1 0 3 0 1 1 1 0 1 0 2 0 1。求该汽车制造商生产的汽车每辆疵点数的总体均值μ的95%的置信区间。
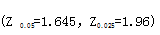
-
已知某生产线在2010年上半年各月发生故障的次数分别为:5、4、7、5、5、4次,计算各月故障次数的平均数和方差。
-
王某从外地来本市参加会议。他乘火车、轮船、汽车、飞机的概率分别为0.3、0.2、0.1、0.4,而他乘火车、轮船、汽车、飞机准时到达的概率分别为0.9、0.6、0.8、0.95。如果他准时到达了,则他乘汽车来的概率是多少。
-
在假设检验中,如果仅仅关心总体均值与某个给定值是否有显著区别,应采用的检验为_________.
-
设一元线性回归方程为
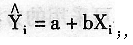 若己知b=2
若己知b=2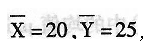 则a等于_________。
则a等于_________。 -
某种股票周二的价格上涨了15%,周三上涨了4%,则两天累计涨幅为_________。
-
随着样本容量的增大,估计量的估计值愈来愈接近总体参数值,我们称此估计量具有 _________.
-
在统计分组中,全部数据在各组内的分配状况被称为_________。
-
使用基期零售价格作权数计算的商品销售量指数
- A.消除了价格变动对指数的影响
- B.消除了销售量变动对指数的影响
- C.单纯反映了商品价格的综合变动
- D.反映了商品价格和销售量的综合变动
-
商品销售额实际增加400元,若由于销售量增长使销售额增加420元,则由于价格
- A.增长使销售额增加20元
- B.增长使销售额增长210元
- C.降低使销售额减少20元
- D.降低使销售额减少210元
-
现象之间相互关系的类型有
- A.函数关系和因果关系
- B.相关关系和因果关系
- C.相关关系和函数关系
- D.回归关系和因果关系
-
已知环比增长速度为2%、5%、6.1%,则定基增长速度为
- A.2%×5%×6.l%
- B.(2%×5%×6.1%)-1
- C.102%×l05%×l06.1%
- D.(102%×l05%×l06.1%)-1
-
产品成本Y对年份X回归后得到回归直线方程为爹=200—2.5x,回归系数b=-2.5表示
- A.时间每增加一个单位,产品成本平均增加2.5个单位
- B.时间每增加一个单位,产品成本平均下降2.5个单位
- C.单位产品每变动一个单位,平均需要2.5个时间单位
- D.时间每减少一个单位,产品成本平均下降2.5个单位
-
在一定的样本容量和抽样方式下,若缩小置信区间则
- A.会降低置信度
- B.会提高置信度
- C.不会影响置信度
- D.可能降低也可能提高置信度
-
对正态总体N(μ,l6)中的均值进行假设检验,可采用的方法为
- A.Z检验
- B.t检验
- C.F检验
- D.X2检验
-
质检部门要求以99%的把握检验某产品次品率P是否低于l%。该质检部门设立的原 假设应该为
- A.H0:P=0.01
- B.H0:P<0.01
- C.H0:P≥O.Ol
- D.H0:P≤O.01
-
在抽样比
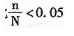 时,对于总体比例估计的样本量的确定,下列说法正确的是
时,对于总体比例估计的样本量的确定,下列说法正确的是- A.样本量将随着允许误差的减小而减小
- B.样本量随着相对误差的减小而减小
- C.样本量将随着置信水平降低而降低
- D.样本量不随置信水平提高而变化
-
在总体方差一定的情况下,在下列样本量中,抽样平均误差最小的是
- A.20
- B.40
- C.60
- D.80
-
设随机变量X服从N(2/3,1),则X的数学期望EX=
- A.1/6
- B.2/3
- C.3/4
- D.1
-
9某批待出口的水果罐头,平均净重是184克,标准差是2.5克。假定罐头的实际净重服从正态分布,现随机抽取l罐,则其实际净重超过l84.5克的概率
- A.大于0.5
- B.等于0.5
- C.小于0.5
- D.大于0.6
-
已知样本方差为S2=100,若将所有样本观察值都乘以1/5,则新的样本方差为
- A.2
- B.4
- C.5
- D.6
-
设A、B为两个事件,P(B)=0.7,
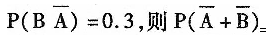
- A.O.3
- B.0.4
- C.0.5
- D.0.6
-
一个服从二项分布的随机变量,其方差与数学期望之比为3/4,则该分布的参数P是
- A.1/4
- B.2/4
- C.3/4
- D.1
-
在一次抛硬币的试验中,小王连续抛了2次,则两次都是正面向上的概率为

- A.A
- B.B
- C.C
- D.D
-
设A、B、C为任意三个事件,则“在这三个事件中A与B不发生但是C发生”可以表示为
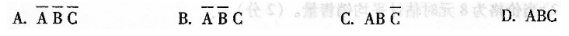
- A.A
- B.B
- C.C
- D.D
-
某公司共有5个推销员,今年8月份这5个推销员的销售额分别为6500元、7300元、 5500元、6000元、7000元,则这5个推销员的平均销售额为
- A.5500元
- B.6460元
- C.6500元
- D.7000元
-
设一个袋子里面有8个编号分别为l~8的球,从中任取一个,观察其编号。用Ω表示 样本空间,用A表示事件“抽到奇数号球”,用8表示“抽到偶数号球”,则A+B=
- A.{1,3,5,7}
- B.{2,4,6,8}
- C.Ω
- D.空集
-
随机抽取5个人,他们的年平均收人是72000元,其中有2人的平均年收入是60000元, 则另外3人的年平均收入为
- A.80000元
- B.82000元
- C.84000元
- D.86000元

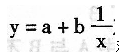 对价格与销售量进行回归分析。
对价格与销售量进行回归分析。
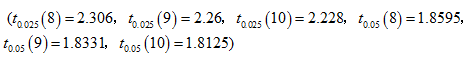

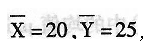 则a等于_________。
则a等于_________。