数量方法(二)2017年4月全国统一真题题试卷(00994)
-
为研究某商品A的销售量与价格之间的关系,调查获得5个月的月销售量与月销售价格的数据如题33表:

(1)以月销售量为因变量,建立回归直线方程;
(2)计算销售量与价格之间的简单相关系数;
(3)当商品的价格由每件1.10元降到每件0.85元时,商品A的销售量将如何变化? 变化多少?
-
从某生产线上随机取9袋产品,已知它们的重量分别为:106,95,104,95,102,97,103,102, 105克。正常情况下该生产线生产的产品重量服从均值为100克的正态分布。
(1)求产品重量的样本均值;
(2)求产品重量的样本方差;
(3)请以95%的可靠程度检验该生产线是否处于正常状态?并给出相应的原假设、备择假设及检验统计量。
-
某集市三种主要商品的贸易额及贸易量变动资料如题31表:
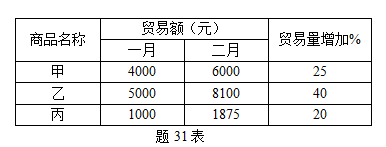
试从相对数与绝对数两个方面分析贸易量对贸易额的影响。
-
某培训中心采用A、B两种相互独立的培训方法对学员进行某门课程的培训。现从采用 A培训方法和采用B培训方法的学员中各自随机抽取了60人,测得他们完成培训后该课程考试的平均分分别为90分和85分,样本标准差分别为8分和5分。求采用A、B两种培训方法培训后该课程平均考试分数之差的置信度为95%的置信区间。
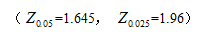
-
某企业在1992年利润为10.1亿元,2000年达到11.3亿元,试问在这期间企业利润年平均增长速度为多少?如果按此利润平均增长速度发展,则2015年企业利润将达到多少亿元?
-
设随机变量X服从区间[-3,3]上的均匀分布,求X的期望和方差。
-
有4盒球,里面装满了红球和蓝球。选取第一、二、三、四个盒子的概率均为0.25。从第一盒中取得红球的概率为0.5,从第二盒取得红球的概率为0.6,从第三盒中取得红球的概率为0.2。这四盒球中任取一球,取得红球的概率为0.4。求从第四盒取得红球的概率。
-
某车间20名工人工龄数据如题26表1所示。
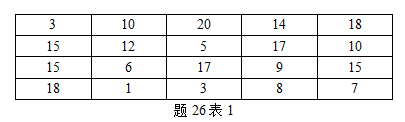
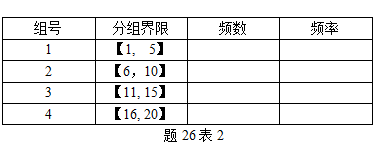
请按照题26表2给出的分组界限进行分组,并按照题26表2给出的格式制作频率分布表。
-
测定循环波动的常用方法是_______。
-
设一元线性回归方程为
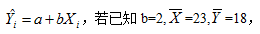 ,则a等于_______。
,则a等于_______。 -
在大样本情况下,对于总体均值的区间估计,若保持置信区间不变,当增大样本容量时,将_______置信水平。
-
设有两个独立正态总体,
 ,为检验
,为检验 分别从两个总体中抽取了容量为
分别从两个总体中抽取了容量为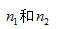 的样本均值分别记为
的样本均值分别记为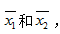 则检验H0的统计量为_______。
则检验H0的统计量为_______。 -
在指数体系中,总量指数与各因数指数之间的数量关系是( )
- A.总量指数等于各因数指数之和
- B.总量指数等于各因数指数之差
- C.总量指数等于各因数指数之积
- D.总量指数等于各因数指数之商
-
下列指数中,属于数量指标指数的有( )
- A.农副产品产量总指数
- B.农副产品收购价格总指数
- C.某种工业产品成本总指数
- D.全部商品批发价格指数
-
一组数据中最大值和最小值之差被称为_______。
-
若已知
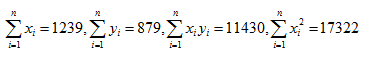 ,n=100,则直线回归方程的回归系数为( )
,n=100,则直线回归方程的回归系数为( )- A.0.27
- B.0.31
- C.0.42
- D.0.53
-
 这一公式适用于( )
这一公式适用于( )- A.时期数列计算序时平均数
- B.间隔相等的时点数列计算序时平均数
- C.间隔不相等的试点数列计算序时平均数
- D.由两个时点数列构成的相对数时间数列计算序时平均数
-
如果相关系数|r|=1,则表明两个变量之间存在着( )
- A.正相关
- B.不相关
- C.负相关
- D.完全相关
-
显著性水平a表达了区间估计的( )
- A.可靠性
- B.不可靠的概率
- C.准确性
- D.有效性
-
某估计量是总体参数的一致性估计量,则以下说法错误的是( )
- A.随着样本容量的增大,该估计量对总体参数真值的估计就愈精确
- B.随着样本容量的增大,该估计量会由有偏估计量变为无偏估计量
- C.可以通过增加样本容量来增加该估计量对总体参数真值估计的可靠性
- D.可以通过增加样本容量来提高该估计量对总体参数真值估计的可精度
-
假设检验中,对总体的未知参数事件先作出的某种确定假设,通常称为( )
- A.原假设
- B.备择假设
- C.对立假设
- D.以上全错
-
在有限总体不重复抽样时,对于总体均值估计的样本量的确定,以下说法正确的是( )
- A.样本量将随着允许误差的增加而减小
- B.样本量将随着置信水平提高而减小
- C.样本量不随允许误差的变化而变化
- D.样本量不随置信水平提高而变化
-
将总体单元在抽样之前按某种顺序排列,并按照设计的规则确定一个随机起点,然后每隔一定的时间隔逐个抽取样本单元的抽选方法称为( )
- A.随机抽样
- B.分层抽样
- C.系统抽样
- D.分群抽样
-
与样本均值的方差成反比的是( )
- A.样本容量
- B.总体的方差
- C.总体的均值
- D.样本值
-
若已知DX=25,DY=9, COV(X,Y)=10.5,则X与Y相关系数r为( )
- A.0.2
- B.0.6
- C.0.7
- D.0.8
-
已知随机变量X与Y有DX=5, DY=12,且COV(X,Y)=2.8,则D(X-Y-6)=( )
- A.8.3
- B.11.4
- C.22.5
- D.26.8
-
事件A、B相互对立,P(A)=0.3,
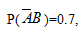 , 则P(A+B)=( )
, 则P(A+B)=( )- A.0
- B.0.3
- C.0.4
- D.1
-
设A、B、C为任意三个事件,则“在这三个事件中A与B同时发生且C不发生”可以表示为( )
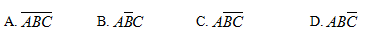
- A.A
- B.B
- C.C
- D.D
-
随机变量X的期望和方差分别表示X取值的( )
- A.绝对值,离散程度
- B.平均值,平均程度
- C.平均值,离散程度
- D.相对值,平均程度
-
将一枚硬币抛掷两次的样本空间Ω={00, 01, 10, 11}(用0表示出现正面,用1表示出现 反面)。则事件“第二次出现反面”可以表示为( )
- A.{00,03}
- B.{10,01}
- C.{11,01}
- D.{10,11}
-
盒子里装了2个红球和3个蓝球,从盒中任取两球,取到一个红球和一个蓝球的概率为
- A.3/5
- B.1/2
- C.6/25
- D.7/10
-
某公司共有7个推销员,今年8月份这7个推销员的销售额分别为5500元、6500元、7300元、5300元、6000元、5500元、7200元,则这7个推销员销售额的中位数为( )
- A.5500元
- B.6000元
- C.6460元
- D.6500元
-
已知某班50名同学《大学英语》平均成绩是80分,该班30名男生的平均成绩是76分,则该班女生的平均成绩是( )
- A.76分
- B.80分
- C.85分
- D.86分




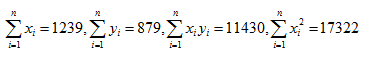 ,n=100,则直线回归方程的回归系数为( )
,n=100,则直线回归方程的回归系数为( ) 这一公式适用于( )
这一公式适用于( )