事件A、B相互对立，P(A)=0.3,, 则P(A+B)=( )

为研究某商品A的销售量与价格之间的关系，调查获得5个月的月销售量与月销售价格的数据如题33表：

(1)以月销售量为因变量，建立回归直线方程;

(2)计算销售量与价格之间的简单相关系数;

(3)当商品的价格由每件1.10元降到每件0.85元时，商品A的销售量将如何变化? 变化多少?

从某生产线上随机取9袋产品，已知它们的重量分别为：106,95,104,95,102,97,103,102, 105克。正常情况下该生产线生产的产品重量服从均值为100克的正态分布。

(1)求产品重量的样本均值;

(2)求产品重量的样本方差;

(3)请以95%的可靠程度检验该生产线是否处于正常状态?并给出相应的原假设、备择假设及检验统计量。

某集市三种主要商品的贸易额及贸易量变动资料如题31表：

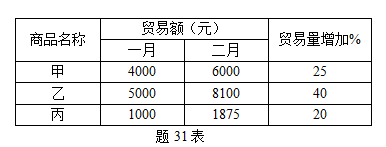
试从相对数与绝对数两个方面分析贸易量对贸易额的影响。

某培训中心采用A、B两种相互独立的培训方法对学员进行某门课程的培训。现从采用 A培训方法和采用B培训方法的学员中各自随机抽取了60人，测得他们完成培训后该课程考试的平均分分别为90分和85分，样本标准差分别为8分和5分。求采用A、B两种培训方法培训后该课程平均考试分数之差的置信度为95%的置信区间。

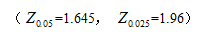
某企业在1992年利润为10.1亿元，2000年达到11.3亿元，试问在这期间企业利润年平均增长速度为多少?如果按此利润平均增长速度发展，则2015年企业利润将达到多少亿元?

设随机变量X服从区间[-3,3]上的均匀分布，求X的期望和方差。

有4盒球，里面装满了红球和蓝球。选取第一、二、三、四个盒子的概率均为0.25。从第一盒中取得红球的概率为0.5，从第二盒取得红球的概率为0.6，从第三盒中取得红球的概率为0.2。这四盒球中任取一球，取得红球的概率为0.4。求从第四盒取得红球的概率。

某车间20名工人工龄数据如题26表1所示。

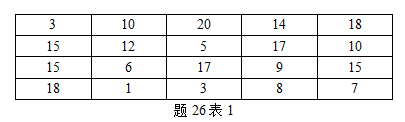
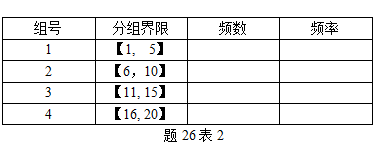
请按照题26表2给出的分组界限进行分组，并按照题26表2给出的格式制作频率分布表。

测定循环波动的常用方法是_______。

设一元线性回归方程为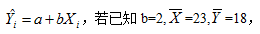，则a等于_______。