全国2013年10月高等教育自学考试《高等数学(一)》试题
-
计算二重积分I=
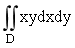 ,其中D是由直线y=2x、x=l及曲线y=x2围成的平面区域.
,其中D是由直线y=2x、x=l及曲线y=x2围成的平面区域.
-
求微分方程
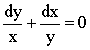 满足初始条件y|x=1=1的特解.
满足初始条件y|x=1=1的特解. -
设z=z(x,y)是由方程z^3-3xyz-1=0所确定的隐函数,求偏导数
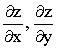 .
. -
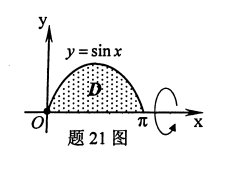
设曲线y=sinx(0≤x≤π)与x轴所围成的平面区域为D.
(1)求D的面积A;
(2)求D绕x轴一周的旋转体体积Vx.
-
计算定积分I=
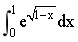 .
. -
求函数f(x)=ln(x2+1)在区间[-1,2]上的最大值和最小值.
-
求曲线y=
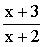 的水平和铅直渐近线.
的水平和铅直渐近线. -
已知函数y=f(sin x),且f具有二阶导数,求y".
-
求a的值,使得函数f(x)=
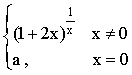 在x=0处连续.
在x=0处连续. -
求函数y=
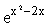 的单调区间.
的单调区间. -
求不定积分
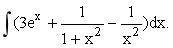
-
设函数y=sin(2x^2+1),求导数
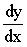 .
. -
已知函数f(x+1)=x^2+2x,求f(x).
-
求极限
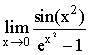 .
. -
设函数z=ln(x^2+y^2),则
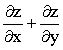 =
=
- A.
- B.
- C.
-
若f(x)是g(x)的一个原函数,则下列选项正确的是

- A.
- B.
- C.
- D.
-
极限
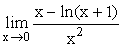 =
=- A.-1/2
- B.0
- C.1/2
- D.1
-
某产品产量为q时总成本C(q)=1100+
 ,则q=1200时的边际成本为
,则q=1200时的边际成本为- A.0
- B.1/2
- C.1
- D.2
-
已知函数f(x)=ax^2-4x+1在x=2处取得极值,则常数a=
- A.0
- B.1
- C.2
- D.3
-
设函数f(x)=arctan(x^2),则导数
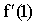 =
=- A.-1
- B.0
- C.1
- D.2
-
函数f(x)=
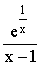 的所有间断点是
的所有间断点是- A.x=0
- B.x=1
- C.X=0,x=-1
- D.x=0,x=1
-
下列等式成立的是

- A.
- B.
- C.
- D.

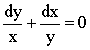 满足初始条件y|x=1=1的特解.
满足初始条件y|x=1=1的特解.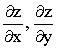 .
.
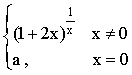 在x=0处连续.
在x=0处连续.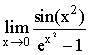 .
.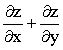 =
=

