高等数学（工本）自考2012年04月真题及答案解析
-
将函数f ( x )=
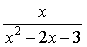展开为x的幂级数. -
设函数z=ln(
+
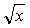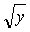)，证明2x
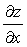+2y
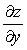=1. -
求函数f ( x, y)=3+14y+32x-8xy-2y^2-10x^2的极值.
-
设α为任意实数，判断无穷级数
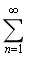
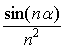的敛散性，若收敛，是绝对收敛还是条件收敛？ -
设函数f ( x )=x^2cosx的马克劳林级数为
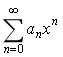，求系数a6. -
求微分方程x
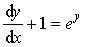的通解. -
验证y1 = e^x,y2 = x都是微分方程（1 – x）
+
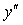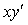-y = 0的解，并写出该微分方程的通解。 -
计算对坐标的曲线积分I=
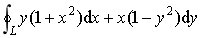，其中L是平面区域D：x2 + y2 ≤4的正向边界. -
计算对弧长的曲线积分I=
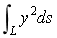，其中L为圆周x^2+y^2=9的左半圆. -
计算三重积分I=
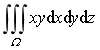，其中积分区域Ω是由x^2+y^2=4及平面z = 0，z = 2所围的在第一卦限内的区域. -
求函数z = x^2 - y^2在点（2，3）处，沿从点A（2，3）到点B（3，3+
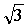）的方向l的方向导数. -
计算二重积分
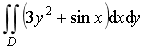，其中积分区域D是由y = | x |和y = 1所围成. -
求曲面z = 2y + ln
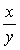在点（1，1，2）处的切平面方程. -
将直线
化为参数式和对称式方程. -
设方程f ( x + y + z, x, x + y)=0确定函数z = z ( x, y ),其中f为可微函数，求
和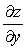
. -
已知
的解，则常数c= ______。 -
幂级数
的收敛半径R=______。 -
函数
的定义域为______。 -
二次积分
，交换积分次序后I=______。 -
已知向量a={-2,c,6}与向量b={1,4,-3}垂直，则常数c= ______。
-
无穷级数
的和为（ ）- A.e + 1
- B.e - 1
- C.e - 2
- D.e + 2
-
微分方程y
=x的阶数是（ ）- A.0
- B.1
- C.2
- D.3
-
已知函数h ( x, y ) = x – y + f ( x + y ),且h (0,y) = y^2,则f ( x + y )为（ ）
- A.y (y + 1)
- B.y (y - 1)
- C.( x + y)( x + y -1)
- D.( x + y )( x + y +1)
-
下列表达式是某函数u(x,y)的全微分的为（ ）
- A.x^2ydx + xy^2dy
- B.xdx + xydy
- C.ydx - xdy
- D.ydx + xdy
-
下列曲面中，母线平行于y轴的柱面为（ ）
- A.z = x^2
- B.z = y^2
- C.z = x^2 + y^2
- D.x + y + z =1
展开为x的幂级数.
+
)，证明2x
+2y
=1.
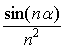的敛散性，若收敛，是绝对收敛还是条件收敛？
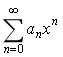，求系数a6.
的通解.
+
-y = 0的解，并写出该微分方程的通解。
，其中L是平面区域D：x2 + y2 ≤4的正向边界.
，其中L为圆周x^2+y^2=9的左半圆.
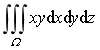，其中积分区域Ω是由x^2+y^2=4及平面z = 0，z = 2所围的在第一卦限内的区域.
）的方向l的方向导数.
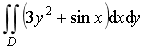，其中积分区域D是由y = | x |和y = 1所围成.
在点（1，1，2）处的切平面方程.
化为参数式和对称式方程.
和
.
的解，则常数c= ______。
的收敛半径R=______。
的定义域为______。
，交换积分次序后I=______。
的和为（ ）
=x的阶数是（ ）