高等数学(工本)自考2013年01月真题及答案解析
-
将函数
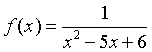 展开为x的幂级数.
展开为x的幂级数. -
求由曲面
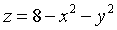 和
和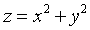 所围成的立体的体积.
所围成的立体的体积. -
从斜边之长为k的一切直角三角形中,求有最大周长的直角三角形.
-
已知f(x)是周期为2π的周期函数,它在[-π,π)上的表达式为

求f(x)傅里叶级数
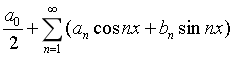 中系数a0.
中系数a0. -
判断无穷级数
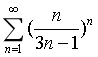 的敛散性.
的敛散性. -
求微分方程
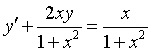 的通解.
的通解. -
求微分方程
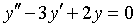 的通解.
的通解. -
计算对坐标的曲面积分
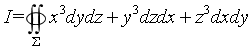 ,其中
,其中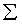 是球面
是球面 的外侧.
的外侧. -
计算三重积分
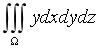 ,其中积分区域Ω是由x=0,y=0,z=0及x+y+z=1所围的.
,其中积分区域Ω是由x=0,y=0,z=0及x+y+z=1所围的. -
验证对坐标的曲线积分
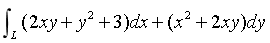 与路径无关,并计算
与路径无关,并计算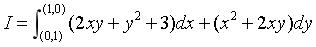 .
. -
设函数
 ,求梯度grad
,求梯度grad .
. -
计算二重积分
 ,其中积分区域D:
,其中积分区域D:
-
求过点P1(-2,3,-1)和P2(3,3,5)的直线方程.
-
设f是可微的二元函数,并且
 ,求全微分dz.
,求全微分dz. -
已知方程
 ,确定函数
,确定函数 ,求
,求 和
和 .
. -
微分方程
 的通解为______。
的通解为______。 -
已知无穷级数
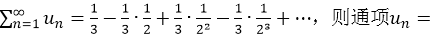 ______。
______。 -
已知向量α(1,-1,1),β(-2,C,-2),并且α×β=0,则常数c=______。
-
已知函数
 ______。
______。 -
设积分区域
 ______。
______。 -
微分方程
 是
是- A.可分离变量的微分方程
- B.齐次微分方程
- C.一阶线性齐次微分方程
- D.一阶线性非齐次微方程
-
下列条件收敛的无穷级数是

- A.
- B.
- C.
- D.
-
点(1,2)是函数
 的
的- A.极小值点
- B.极大值点
- C.最大值点
- D.间断点
-
设积分曲线L:y=1+x(0≤x≤1),则对弧长的曲线积分


- A.
- B.
- C.
- D.
-
在空间直角坐标系中,点(2,-1,4)到oyz坐标面的距离为
- A.1
- B.2
- C.4
- D.

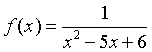 展开为x的幂级数.
展开为x的幂级数.
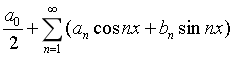 中系数a0.
中系数a0.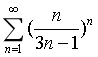 的敛散性.
的敛散性.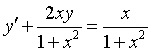 的通解.
的通解.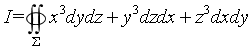 ,其中
,其中 ,其中积分区域D:
,其中积分区域D: ______。
______。
