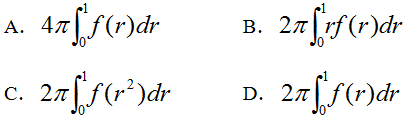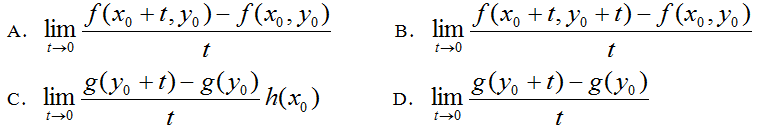高等数学(工本)自考2016年04月真题及答案解析
-
证明对坐标的曲线积分
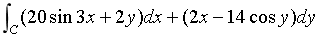 在整个xoy面内与路径无关。
在整个xoy面内与路径无关。 -
将函数
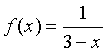 展开为x的幂级数。
展开为x的幂级数。 -
某工厂生产的两种商品的产量x和y的利润函数为
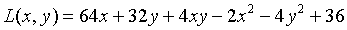
求获得最大利润时两种商品的产量,并求最大利润。
-
判断无穷级数
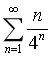 的敛散性。
的敛散性。 -
已知
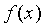 是周期为2π的周期函数,它在
是周期为2π的周期函数,它在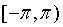 上的表达式为
上的表达式为
求
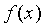 傅里叶级数
傅里叶级数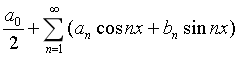 中系数
中系数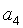 。
。 -
计算对坐标的曲线积分
 ,其中C为直线y=x从点O(0,0)到点A(1,1)的线段。
,其中C为直线y=x从点O(0,0)到点A(1,1)的线段。 -
求微分方程
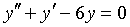 的通解。
的通解。 -
求微分方程
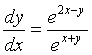 的通解。
的通解。 -
计算对弧长的曲线积分
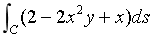 ,其中C是从点A(-1,-1)到B(-1,2)的直线段。
,其中C是从点A(-1,-1)到B(-1,2)的直线段。 -
计算二重积分
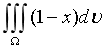 ,其中
,其中 是由曲面
是由曲面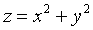 和
和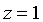 所围成的区域。
所围成的区域。 -
计算二重积分
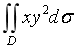 ,其中D是由
,其中D是由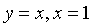 及
及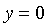 所围成的区域。
所围成的区域。 -
求函数
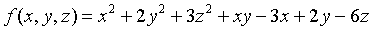 在点
在点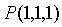 处的梯度
处的梯度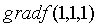 。
。 -
求过点
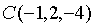 并且垂直于平面
并且垂直于平面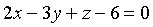 的直线方程。
的直线方程。 -
求曲线
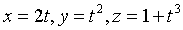 在对应于
在对应于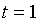 的点处的法平面方程。
的点处的法平面方程。 -
求函数
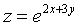 的全微分dz。
的全微分dz。 -
已知无穷级数
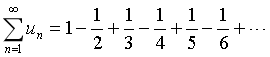 ,则
,则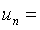 _____________。
_____________。 -
曲线
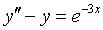 的特解
的特解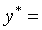 _____________。
_____________。 -
点
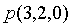 到平面
到平面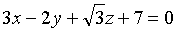 的距离为_____________。
的距离为_____________。 -
已知函数
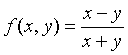 ,则
,则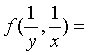 _____________。
_____________。 -
设积分区域
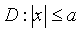 ,
,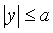 ,且二重积分
,且二重积分 ,则常数a=_____________。
,则常数a=_____________。 -
设无穷级数
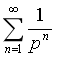 收敛,则在下列数值中的取值为
收敛,则在下列数值中的取值为- A.1/3
- B.1/2
- C.1
- D.2
-
微分方程
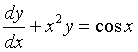 是
是- A.可分离变量的微分方程
- B.齐次微分方程
- C.一阶线性齐次微分方程
- D.一阶线性非齐次微分方程
-
设积分区域
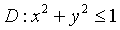 ,则二重积分
,则二重积分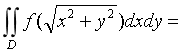
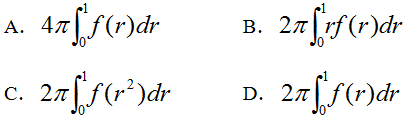
- A.
- B.
- C.
- D.
-
设函数
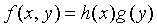 在点
在点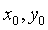 的某领域内有定义,且存在一阶偏导数,则
的某领域内有定义,且存在一阶偏导数,则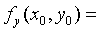
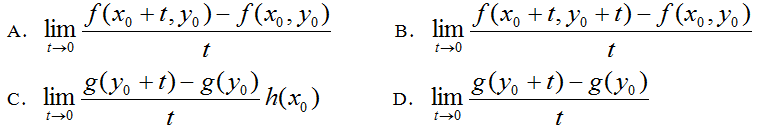
- A.
- B.
- C.
- D.
-
直线
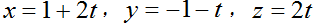 的方向向量是
的方向向量是- A.{2,-1,2}
- B.{2,1,2}
- C.{-1,1,0}
- D.{1,-1,0}
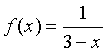 展开为x的幂级数。
展开为x的幂级数。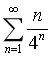 的敛散性。
的敛散性。
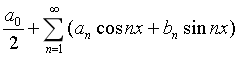 中系数
中系数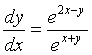 的通解。
的通解。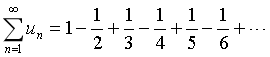 ,则
,则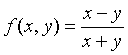 ,则
,则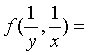 _____________。
_____________。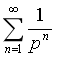 收敛,则在下列数值中的取值为
收敛,则在下列数值中的取值为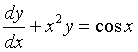 是
是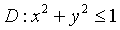 ,则二重积分
,则二重积分