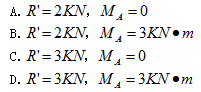工程力学(二)2017年4月真题(02391)
-
一圆形截面杆受力如图所示,已知水平外力F=100KN,杆长ι=1m,直径d=5cm,材料的许用应力[σ]=160MPa。试校核该杆的强度。
-
图示结构中,①杆和②杆的直径均为d,铅垂力F=10KN,许用应力[σ]=160MPa。试求杆直径d的最小值。
-
用型号为20a号工字钢制成的梁如图所示,材料的许用应力[σ]=160MPa,已知抗弯截面模量
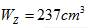 。试求最大荷载[F]。
。试求最大荷载[F]。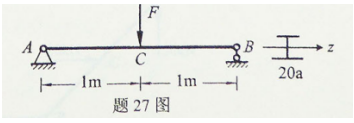
-
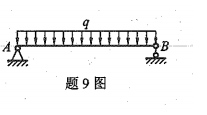
简支梁AB所受外荷载及尺寸如图所示,试画出该梁的剪力图和弯矩图。
-
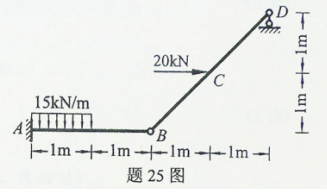
结构尺寸及受理如图所示,求固定端A处约束反力。
-
图示轴向拉杆,已知轴向外力F=10KN,弹性模量
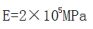 ,长度ι=20cm,横截面积
,长度ι=20cm,横截面积 。试求杆BC段的平均线应变
。试求杆BC段的平均线应变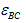 。
。
-
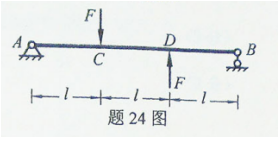
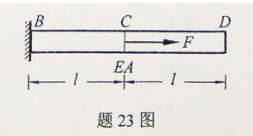
梁AD上作用外力及尺寸如图所示,求A和D处的支座反力。
-
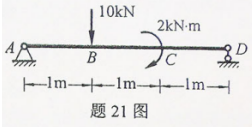
如图所示,已知A、B两点力的大小为:
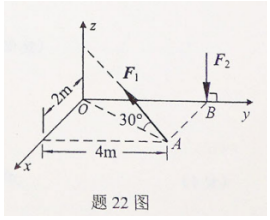
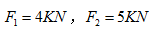 求二力对坐标轴x、y和z之矩的代数和
求二力对坐标轴x、y和z之矩的代数和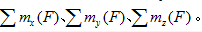 。
。
-
图示单元体的最大主应力=( )。
-
图材料的破坏形式可主要归结为脆性断裂和塑性屈服两大类型。第三强度理论适用于( )。
-
图已知图(a)所示简支梁B截面转角
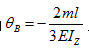 ,则图(b)所示简支梁B截面转角
,则图(b)所示简支梁B截面转角 =( )。
=( )。
-
弯曲梁的挠度与梁所受的荷载大小成( )比。
-
图示受扭圆杆,抗扭刚度为
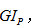 ,则该杆最大单位长度相对扭转角
,则该杆最大单位长度相对扭转角 ( )。
( )。
-
低碳钢在轴向拉伸时,变形发展的四个特征阶段分别为:弹性阶段、( )、强化阶段和颈缩阶段。
-
杆AC在图示四个力作用下平衡。F1、F2和F3未知。用三矩式平衡方程
 ,
, 和不能求出大小的未知力是( )。
和不能求出大小的未知力是( )。
-
在刚体上加上一平衡力系不影响( )力系的作用效果。
-
力偶中两个力所在的平面称为力偶( )。
-
某图示某纯弯曲梁的横截面,已知M点的正应力
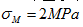 ,则N点的正应力σN为()
,则N点的正应力σN为()
- A.2MPa
- B.4MPa
- C.6MPa
- D.8MPa
-
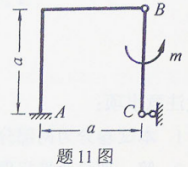
结构尺寸如图所示,力偶矩m和尺寸a为已知,则固定端A处的约束反力偶矩的大小等于( )。
-
细长压杆的临界应力为()
- A.小于或等于比例极限σP
- B.大于比例极限σP
- C.大于比例极限σP,小于屈服极限σS
- D.大于屈服极限σP
-
图示单向应力状态下
 ,x轴的方向线应变为()
,x轴的方向线应变为()
- A.小于零
- B.等于零
- C.大于零
- D.不能确定
-
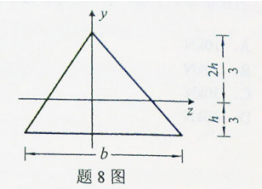
图示截面对z轴过形心,则该这图形对z轴的静矩Sz为()

- A.
- B.
- C.
- D.
-
图示结构为()
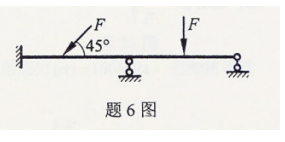
- A.三次超静定结构
- B.二次超静定结构
- C.一次超静定结构
- D.静定结构
-
材料的切变模量G、拉压弹性模量E和泊松比μ之间的关系为()
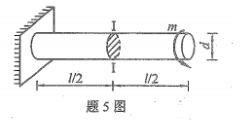
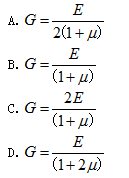
- A.
- B.
- C.
- D.
-
如图所示,直角曲杆ABC上C点作用有水平力F,则A支座的约束反力方向应为()

- A.水平向左
- B.铅垂向下
- C.沿AC方向,指向C点
- D.沿AC方向,背离C点
-
如图所示,物体A的重量W=8KN,物体A与接触面的静滑动摩擦系数f=0.2,若使物体不下滑,水平压力F的最小值为()

- A.10KN
- B.20KN
- C.30KN
- D.40KN
-
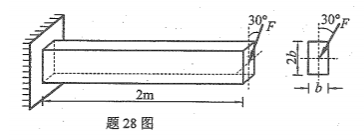
如图所示,平面任意力系由F1、F2和F3三个力组成,F1=3KN、F2=F3=2KN,则该力系向A点简化的主矢和主矩的大小分别为()

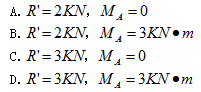
- A.
- B.
- C.
-
如图所示,平面汇交力系由F1、F2两个力组成
 已知该力系的合力在y轴上的投影Ry=0,则力F2的大小为()
已知该力系的合力在y轴上的投影Ry=0,则力F2的大小为()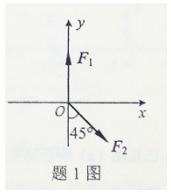
- A.0
- B.10KN
- C.20KN
- D.30KN







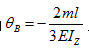 ,则图(b)所示简支梁B截面转角
,则图(b)所示简支梁B截面转角