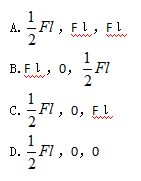工程力学(二)2005年4月真题(02391)
-
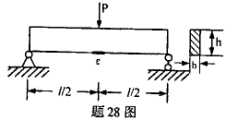
矩形截面简支梁受力如图所示,l、b、h和材料的弹性模量E均为已知,现测得梁跨中截面下边缘处的纵向线应变为ε,试求荷载P。
-
混合结构受载荷P和P′=1/2P共同作用,如图所示。试求结构的支座反力及l杆和2杆的轴力。

-
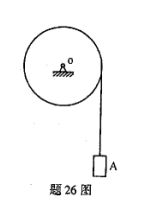
匀质圆轮质量为2m,半径为R,绕中心轴O转动,它通过无重软绳联接一质量为m的物块A.
(1)用动量矩定理求物块A的加速度aA;
(2)用动量定理求轴O的反力YO。
-
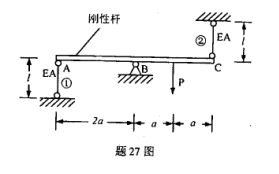
图示结构中,杆①和杆②的抗拉剐度均为EA,水平杆为刚性杆,试求杆①和杆②的内力。
-
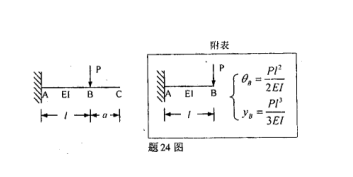
试用叠加法求图示粱C截面的转角和挠度。
-
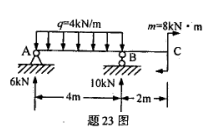
ABC梁的支座反力值已算出,如图所示。试绘出该梁的剪力图和弯矩图。
-
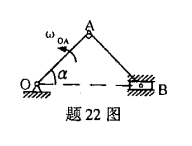
图示曲柄连杆机构中,已知α、ωOA,OA=AB=L,用瞬心法求连杆AB的角速度ωAB及滑块B的速度VB。
-
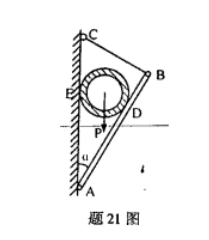
已知重量为P的圆管用AB杆和绳BC固定在铅垂墙壁上,如图所示。AB杆与墙面间的夹角为α,求AB杆对圆管的支承力。
-
按强度理论校核杆件强度时,第三、第四强度理论适用于( )材料。
-
计算压杆临界力的欧拉公式
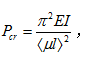 ,只适用于( )杆。
,只适用于( )杆。 -
对偏心受压杆,当纵向外力的作用点位于( )范围内时,其横截面上只产生压应力。
-
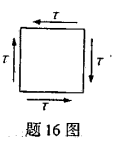
某单元体上的应力情况如图所示,用第三强度理论校核该点强度时,其相当应力口σr3为 。
-
质量为m的矩形方板用等长且平行的二杆悬挂,如图所示。设杆长为ι,杆的角速度ω=0,角加速度为
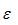 ,则该瞬时方板惯性力系的主矩的值
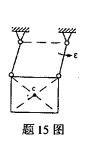
,则该瞬时方板惯性力系的主矩的值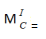 ( )。
( )。
-
圆形截面铸铁杆受扭破坏时,沿斜截面破坏,这是由( )应力引起的。
-
圆轮中心为O,半径为R,轮上的绳连接一刚度系数为k的弹簧,并固定在地面上。初始弹簧无变形,在圆盘上加一矩为m(常量)的力偶,使圆盘转过角度φ,则此过程中弹性力的功等于( )。
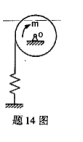
-
匀质圆轮C质量为m,半径为R,在倾角为α的斜面上作纯滚动,其角速度为ω.轮C的动能T=( )。
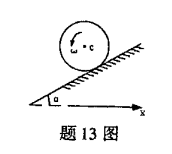
-
已知力F=10kN和力偶m=5000N·m作用在某刚体的同一平面内,如图所示。为将其简化为一个力,须将力F向右平移( )米。
-
定轴转动刚体上一点的加速度可分解为( )两项。
-
长度、直径,材料均相同的各轴向受压圆杆如图所示,其临界力最大者为()
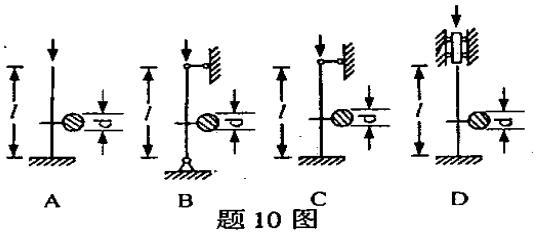
- A.A
- B.B
- C.C
- D.D
-
圆形截面杆受扭如图所示,杆中的最大剪应力为()
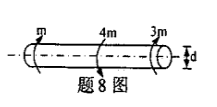
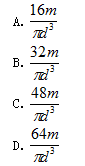
- A.A
- B.B
- C.C
- D.D
-
受横向力作用的槽形截面梁如图所示,该梁的变形为()
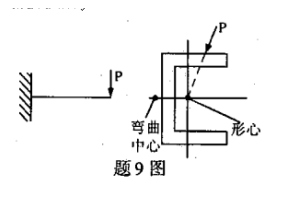
- A.平面弯曲
- B.斜弯曲
- C.平面弯曲与扭转的组合
- D.斜弯曲与扭转的组合
-
①、②、③、④四种材料的应力应变图分别如图所示,材料的弹性模量E值最大者为()
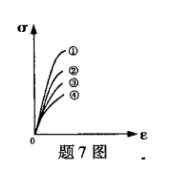
- A.①
- B.②
- C.③
- D.④
-
横截面面积相等、材料不同的两等截面直杆,承受相同的轴向拉力,则两杆的()
- A.轴力相同,横截面上的正应力不同
- B.轴力相同,横截面上的正应力也相同
- C.轴力不同,横截面上的正应力相同
- D.轴力不同,横截面上的正应力也不同
-
图示机构中∠α<45°,则滑块A的虚位移δrA与滑块B的虚位移δrB二者之间的关系应是()
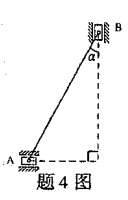
- A.δrA<δrB
- B.δrA =δrB
- C.δrA >δrB
- D.比值δrA:δrB与∠α值无关
-
当用弧坐标形式的运动方程S=S(t)给定动点的运动时,必须具备的条件是()
- A.点作曲线运动
- B.已知运动轨迹,并在其上选定参考点和正、负向
- C.选定坐标轴x和y
- D.只需给定动点的轨迹
-
已知力F作用在直角折杆ABC的自由端C处,方向铅垂向下,如图所示。AB部分长度为ι,BC部分长度为ι/2,A端为固定端,则力F对图示x、y、z轴之矩的值分别为()
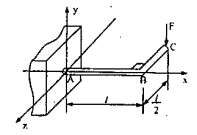
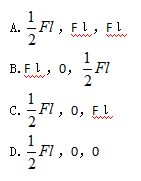
- A.,Fι,Fι
- B.Fι,0,
- C.,0,Fι
- D.,0,0
-
点A作直线运动,其速度为VA=VA(t);点B作圆周运动,其速度为VB=VB(t)。已知两点速度的数值恒相等,则必有()
- A.两点加速度的数值恒相等
- B.两点的法向加速度数值恒相等
- C.B点的切向加速度与A点的加速度恒相等
- D.B点切向加速度的数值与A点加速度的数值恒相等
-
平面汇交力系、平面任意力系、空间汇交力系、空间任意力系的独立的平衡方程的数目分别为()
- A.2,3,3,6
- B.3,3,4,6
- C.3,4,3,6
- D.2,3,4,5








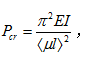 ,只适用于( )杆。
,只适用于( )杆。