离散数学2015年4月考试真题(02324)

设图G如题33图所示，证明：图G不是哈密顿图。

如果小明没有去上学，那他一定是生病了。如果小明生病了，他就会在家休息。只要小明去上学，他就会在教室认真学习。小明要么在教室认真学习，要么在家休息。符号化上述推理过程，并构造推理证明。

用Kruskal算法求题35图中的一棵最小生成树，并画出此树。(须写出详细过程)

在整数集Z上定义一个二元运算 * ，使得对于Z中的任意元素a和b，都有a*b=a+b+ab，证明：是独异点。

设解释 I如下：D ={2,3}，已知F(2,2)=F(3,3)=0，F(2,3)=F(3,2)=1，f(2,2)=f(2,3)=2， f(3,2)=f(3,3)=3。

设A、B是任意集合，证明：~(A∪B)=~A ∩ ~B。

设，≤>为偏序集，其哈斯图如题28图所示，试求：

(1)写出偏序关系≤;

(2)设B={c，d，f}，求B的极大元、极小元、上界和下界。

已知集合S={{1，2，4}，{3}，{5}}是集合={1，2，3，4，5}的一个划分，

(1)写出由S导出的A上的等价关系P;

(2)求P的关系矩阵M_P。

设图G如题25图所示，则图G的邻接矩阵M=_______。

设无向树r有4个度数为3的结点，其余结点都为树叶，则T的树叶数为_______。

?A={a，b，c，d}，B={1，2，3，4}，A到B的关系R={，4>，<6，1>，

2>}，B到A的关系S={<4，a>，<2，b>， <3，b>}，则R。S=_____________。

设集合A={a，b，c}以及A上的一个二元关系R={，b>，，c>，}，则

自反闭包r（R）=___________， 对称闭包s（R）=____________。

设p（A）是非空集合A的幂集，代数系统的零元是_______，幺元是

_______。

设A = {1，2，3}，B = {3，4，5}，则B-A=________，B⊕A=________。

设R={<1,b>,<2,a>,<2,d>,<4,d>}是集合A={1，2，3，4}到集合B={a，b，c，d}的关系，则ranR=_______，domR=_________。

连通图G是一棵树的充要条件是()

• A.有些边不是割边
• B.每条边都是割边
• C.无边割集
• D.每条边都不是割边

• A.
• B.
• C.
• D.

在自然数集N上，下列满足结合律的运算是()

• A.a*b=a^b
• B.a*b=|a+b|
• C.a*b=b
• D.a*b=a+2b

，≤>是一个偏序集，其中A={2，3，6，12，24，36}，≤为A上的整除关系，则

覆盖元素6的元素是（）

• A.6
• B.12
• C.24
• D.36

设集合A有3个元素，则A上的等价关系的个数为()

• A.3个
• B.4个
• C.5个
• D.6个

有界格如9图所示，择元素 d的补元素是()

• A.a
• B.b
• C.c
• D.1

给定A={1，2，3，4}，考虑A上的关系R，若R={(1，3)，(1，4)，(2，3)，(2，4)，(3，4)}，则R是()

• A.自反的
• B.对称的
• C.传递的
• D.反自反的

设R(x)：x是实数;p(x)：x的平方;L(x)：x大于等于0;语句“实数的平方大于等于0”可符号化为()

• A.
• B.
• C.
• D.

设α，β是集合A上的等价关系，则下列关系不一定是等价关系的是()

• A.α。β
• B.α∩β
• C.α∪β
• D.α^-1

下列语句为假命题的是()

• A.如果3是偶数，那么1/3就是有理数
• B.只要3是偶数，1/3就是有理数
• C.除非1/3是有理数，否则3不是偶数
• D.只有3是偶数，1/3才是有理数

设简单无向图G有16条边，有3个4度顶点，有4个2度顶点，其余顶点的度数均大于3，则G中的顶点个数至多为()

• A.9个
• B.10个
• C.11个
• D.12个

设R₁，R₂都是从集合A到B的二元关系，则下列各式成立的是()

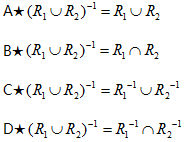
• A.
• B.
• C.
• D.

设p：天下雨;q：我走路上班。命题“只有不下雨，我才走路上班”可符号化为()

• A.p→q
• B.q→p
• C.￢p→q
• D.q→￢p

• A.
• B.
• C.
• D.

设有一个连通平面图G，共有6个面，13条边，则G的顶点个数为()

• A.6
• B.7
• C.8
• D.9