离散数学2010年4月考试真题（02324）

将下面命题符号化，并构造推理证明：所有有理数是实数，有些有理数是整数，所以有些实数是整数。

某城市拟在六个区之间架设有线电话网，其网点间的距离如下列有权矩阵给出，请绘出有权图，给出架设线路的最优方案，并计算线路的总长度。

证明整数集Z上的大于等于关系“≥”是一个偏序关系。

设H是G的非空子集，则是群的子群当且仅当对任意a，b∈H有

求的所有生成元及所有2阶、3阶子群，其中⊕为模7乘法。

用矩阵的方法求右图中结点v₁，v₃之间长度为2的路径的数目。

用推理方法证明：

求右图所示格的所有5元和6元子格。

设A={1,2,3,4}，给定A上的二元关系R={<1,2>,<2,1>,<2,3>,<3,4>}，求R的传递闭包。

n点完全图记为K_n，那么当________时，K_n是平面图，当_____时，K_n是非平面图。

列出的真值表。

用等值演算求的主析取范式。

代数系统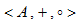是域，则________和________都是交换群。

若图中存在________，它经过图中所有的________，则称该图为汉密尔顿图。

设A={1，2，3，4}，A上的二元关系R={<1，2>，<2，3>，<3，2>}， S={<1，3>，<2，3>，<4，3>}，则R ∩ S=________，=________。

设A={1，2，3，4}，B={2，4，6}，则A-B=________，A⊕B=________。

给出A={1，2}上的一个等价关系________，并给出其对应的划分________。

在谓词推理过程中，由得到P(a)，其中a为论域的某个个体，用的是 ________规则，记为________规则。

请用联结词表示联结词和联结词：________，________。

n个命题变元的________称为大项，其中每个变元与它的否定不能同时出现，但两者必须________。

一棵树有5个3度结点，2个2度结点，其它的都是1度结点，那么这棵树的结点数是( )

• A.13
• B.14
• C.16
• D.17

请写出表示分配律的两个命题公式等价定理________,________。

下列可一笔画成的图形是( )

• A.
• B.
• C.
• D.

右图的最大入度是( )

• A.0
• B.1
• C.2
• D.3

下列说法不正确的是( )

• A.在实数集上，乘法对加法是可分配的
• B.在实数集上，加法对乘法是可分配的
• C.在某集合的幂集上，∪对 ∩ 是可分配的
• D.在某集合的幂集上，∩ 对∪是可分配的

设A是整数集，下列说法正确的是( )

• A.
• B.
• C.
• D.

设A是奇数集合，下列构成独异点的是( )

• A.
• B.
• C.
• D.

下列关系矩阵所对应的关系具有反自反性的是( )

• A.
• B.
• C.
• D.

设R₁和R₂是集合A上的相容关系，下列关于R₁⊕R₂的说法正确的是( )

• A.一定是相容关系
• B.一定不是相容关系
• C.可能是也可能不是相容关系
• D.一定是等价关系

设是正整数集合，则( )

• A.仅是入射
• B.仅是满射
• C.是双射
• D.不是函数

设论域为{1，2}，与公式等价的是( )

• A.A(2)
• B.A(2)
• C.
• D.A(1)

对于公式，下列说法正确的是( )

• A.y是自由变元
• B.x是约束变元
• C.的辖域是
• D.的辖域是P(x,y)

设给定赋值N如下：个体域为自然数集;特定元素a=0;特定函数f(x，y)=x+y，g(x，y)=xy;特定谓词F(x，y)为x=y。在赋值N下，下列公式为真的是( )

• A.
• B.
• C.
• D.

下列式子为矛盾式的是( )

• A.
• B.
• C.
• D.

下列式子不是谓词合式公式的是( )

• A.
• B.
• C.
• D.

下列句子为命题的是( )

• A.全体起立!
• B.x=0
• C.我在说谎
• D.张三生于1886年的春天