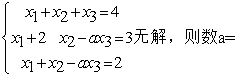线性代数(经管类)2017年10月真题试题及答案解析（04184）

证明矩阵

设矩阵

设3元齐次线性方程组

已知

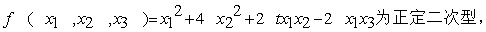
(1)确定矩阵t的取值范围

(2)写出二次型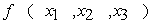的规范形

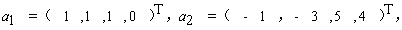
求向量组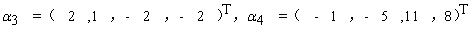的一个极大线性无关组，并将向量组中的其余向量用该极大线性无关组线性表出。

已知矩阵A，B满足AX=B，其中

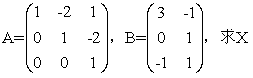
计算4阶行列式

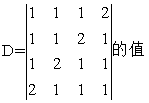
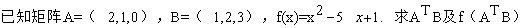
已知3阶实对称矩阵A的特征多项式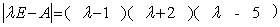，则二次型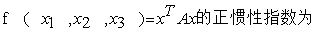

已知3阶矩阵A的特征值1,2,3，且矩阵B与A相似，则|B²+E|=

已知矩阵向量组

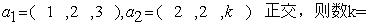
已知线性方程组

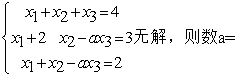
设向量α=(1,1,3)，β=(1，-1,1)，矩阵A=α^Tβ，则矩阵A的非零特征值为

设A为3阶矩阵，将A的第一行与第二行交换得到矩阵B，则|A-B|=.

设n阶矩阵A的所有元素都是1，则R(A)=

设3维向量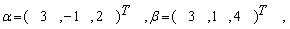若向量γ满足2α+γ=3β，则γ=

设A为3阶矩阵，|A|=1，则|-2A|=.

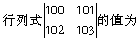
设向量组α₁=(1,2,3)，α₂=(0,1,2)，α₃=(0,0,1),β=(1,3,6), 则( )

• A.α₁,α₂,α₃,β线性无关
• B.β不能由α₁,α₂,α₃线性表示
• C.β可由α₁,α₂,α₃线性表示，且表示法惟一
• D.β可由α₁,α₂,α₃线性表示，但表示法不惟一

设A为4*5矩阵且r(A)=4,则齐次线性方程组AX=0的基础解系中所含向量的个数为( )

• A.1
• B.2
• C.3
• D.4

设3阶矩阵A的特征多项式为|λE-A|=(λ-2)(λ+3)²，则|A+E|=( )

• A.-18
• B.-12
• C.12
• D.18

设A，B是n阶矩阵，下列等式中正确的是( )

• A.
• B.
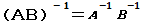
• C.
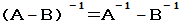
• D.

设A为3阶矩阵且r(A)=1,,则r(BA)=( )

• A.0
• B.1
• C.2
• D.3