线性代数(经管类)2011年7月真题试题及答案解析(04184)
-
求正交变换Y=PX,化二次型f(x1,x2,x3)=2x1x2+2x1x3-2x2x3为标准形.
-
设
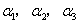 线性无关,证明
线性无关,证明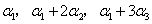 也线性无关.
也线性无关. -
已知1,1,-1是三阶实对称矩阵A的三个特征值,向量
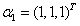 、
、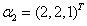 是A的对应于
是A的对应于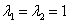 的特征向量,求A的属于
的特征向量,求A的属于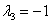 的特征向量.
的特征向量. -
当λ为何值时,齐次方程组
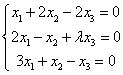 有非零解?并求其全部非零解.
有非零解?并求其全部非零解. -
求向量组:
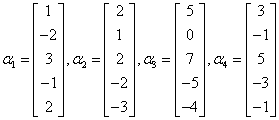 的秩,并给出该向量组的一个极大无关组,同时将其余的向量表示成该极大无关组的线性组合.
的秩,并给出该向量组的一个极大无关组,同时将其余的向量表示成该极大无关组的线性组合. -
计算4阶行列式D=
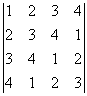 .
. -
设A=
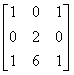 ,而X满足AX+E=A2+X,求X.
,而X满足AX+E=A2+X,求X. -
与矩阵
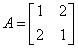 相似的对角矩阵是.
相似的对角矩阵是. -
设A相似于
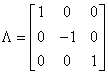 ,则A4=
,则A4= -
二次型f(x1,x2,x3)=x1x2-x1x3+x2x3的矩阵是
-
已知A相似于
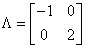 ,则|A-E|=______.
,则|A-E|=______. -
矩阵
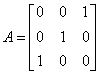 的特征值是 .
的特征值是 . -
三元方程x1+x3=1的通解是 .
-
矩阵
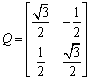 的逆矩阵是 .
的逆矩阵是 . -
设
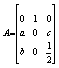 ,且秩(A)=3,则a,b,c应满足 .
,且秩(A)=3,则a,b,c应满足 . -
设A=(-1,1,2)T,B=(0,2,3)T,则|ABT|= .
-
设三阶矩阵
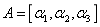 ,其中
,其中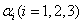 为A的列向量,且|A|=2,则
为A的列向量,且|A|=2,则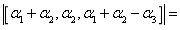 .
. -
设实二次型
 ,则f( )
,则f( )- A.正定
- B.不定
- C.负定
- D.半正定
-
设A=
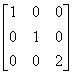 ,则下列矩阵中与A相似的是( )
,则下列矩阵中与A相似的是( )- A.
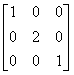
- B.
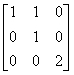
- C.
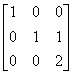
- D.
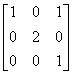
- A.
-
若方程组
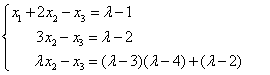 有无穷多解,则=( )
有无穷多解,则=( )- A.1
- B.2
- C.3
- D.4
-
设矩阵A=
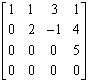 ,则秩(A)=( )
,则秩(A)=( )- A.1
- B.2
- C.3
- D.4
-
实数向量空间V={(x1,x2,x3)|x1+x3=0}的维数是( )
- A.0
- B.1
- C.2
- D.3
-
若方程组
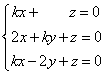 仅有零解,则k=( )
仅有零解,则k=( )- A.-2
- B.-1
- C.0
- D.2
-
设A,B,X,Y都是n阶方阵,则下面等式正确的是( )
- A.若A2=0,则A=0
- B.(AB)2=A2B2
- C.若AX=AY,则X=Y
- D.若A+X=B,则X=B-A
-
设A,B为n阶方阵,且AT=-A,BT=B,则下列命题正确的是( )
- A.(A+B)T=A+B
- B.(AB)T=-AB
- C.A2是对称矩阵
- D.B2+A是对称阵
-
设
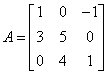 ,则|AAT|=( )
,则|AAT|=( )- A.-49
- B.-7
- C.7
- D.49
-
设A为3阶方阵,且|A|=2,则|-2A|=( )
- A.-32
- B.-8
- C.8
- D.32
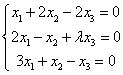 有非零解?并求其全部非零解.
有非零解?并求其全部非零解.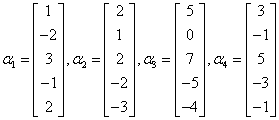 的秩,并给出该向量组的一个极大无关组,同时将其余的向量表示成该极大无关组的线性组合.
的秩,并给出该向量组的一个极大无关组,同时将其余的向量表示成该极大无关组的线性组合. .
. ,而X满足AX+E=A2+X,求X.
,而X满足AX+E=A2+X,求X.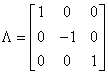 ,则A4=
,则A4=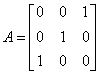 的特征值是 .
的特征值是 .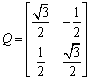 的逆矩阵是 .
的逆矩阵是 . ,且秩(A)=3,则a,b,c应满足 .
,且秩(A)=3,则a,b,c应满足 . ,则下列矩阵中与A相似的是( )
,则下列矩阵中与A相似的是( )



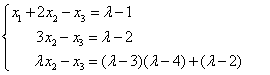 有无穷多解,则=( )
有无穷多解,则=( ) ,则秩(A)=( )
,则秩(A)=( )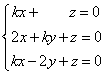 仅有零解,则k=( )
仅有零解,则k=( )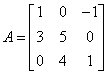 ,则|AAT|=( )
,则|AAT|=( )