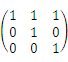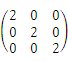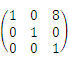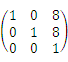线性代数(经管类)2011年4月真题试题及答案解析(04184)
-
已知矩阵A相似于对角矩阵Λ=
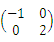 ,求行列式|A-E|的值.
,求行列式|A-E|的值. -
设A为n阶对称矩阵,B为n阶反对称矩阵.证明:
(1)AB-BA为对称矩阵;
(2)AB+BA为反对称矩阵.
-
判断线性方程组
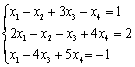 是否有解,有解时求出它的解.
是否有解,有解时求出它的解. -
已知2阶矩阵A的特征值为λ1=1,λ2=9,对应的特征向量依次为α1=(-1,1)T,α2=(7,1)T,求矩阵A.
-
求向量组α1=(1, 2, 1, 0)T,α2=(1, 1, 1, 2)T,α3=(3, 4, 3, 4)T,α4=(4, 5, 6, 4)T的秩与一个极大线性无关组.
-
已知矩阵A=
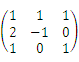 ,B=
,B= ,求:(1)ATB;(2)|ATB|.
,求:(1)ATB;(2)|ATB|. -
设A=
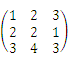 ,B=
,B=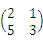 ,C=
,C=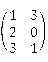 ,且满足AXB=C,求矩阵X.
,且满足AXB=C,求矩阵X. -
设n阶矩阵A的各行元素之和均为0,且A的秩为n-1,则齐次线性方程组Ax=0的通解为 .
-
设3阶矩阵A与B相似,若A的特征值为
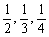 ,则行列式|B-1|=_________.
,则行列式|B-1|=_________. -
设A=
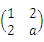 是正定矩阵,则a的取值范围为_______.
是正定矩阵,则a的取值范围为_______. -
设向量α=(1,2,3,4),则α的单位化向量为 .
-
已知3维向量α=(1,-3,3),β=(1,0,-1)则α+3β= .
-
设3阶方阵A的行列式|A|=1/2,则|A3|=
-
设A,B为n阶方阵,且AB=E,A-1B=B-1A=E,则A2+B2= .
-
设矩阵A=
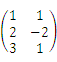 ,B=(1,2,3),则BA= .
,B=(1,2,3),则BA= . -
行列式
 中第4行各元素的代数余子式之和为_________.
中第4行各元素的代数余子式之和为_________. -
行列式
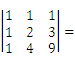 __________.
__________. -
二次型
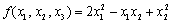 的矩阵为( )
的矩阵为( )- A.
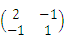
- B.
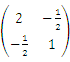
- C.
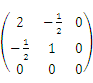
- D.
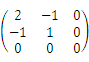
- A.
-
设矩阵A=
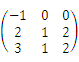 ,则A的对应于特征值λ=0的特征向量为( )
,则A的对应于特征值λ=0的特征向量为( )- A.(0,0,0)T
- B.(0,2,-1)T
- C.(1,0,-1)T
- D.(0,1,1)T
-
向量组
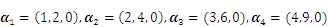 的极大线性无关组为( )
的极大线性无关组为( )- A.
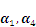
- B.
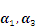
- C.
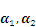
- D.
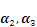
- A.
-
设矩阵A=
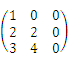 ,那么矩阵A的列向量组的秩为( )
,那么矩阵A的列向量组的秩为( )- A.3
- B.2
- C.1
- D.0
-
设λ=3是可逆矩阵A的一个特征值,则矩阵
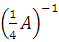 有一个特征值等于( )
有一个特征值等于( )- A.
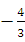
- B.
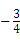
- C.

- D.

- A.
-
设A为3阶矩阵,A的秩r(A)=3,则矩阵A*的秩r(A*)=( )
- A.0
- B.1
- C.2
- D.3
-
设向量
 ,若有常数a,b使
,若有常数a,b使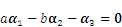 ,则( )
,则( )- A.a=-1, b=-2
- B.a=-1, b=2
- C.a=1, b=-2
- D.a=1, b=2
-
设A、B均为n阶可逆矩阵,且C=
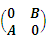 ,则C-1是( )
,则C-1是( )- A.
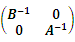
- B.
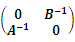
- C.
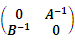
- D.
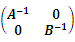
- A.
-
下列等式中,正确的是( )
- A.
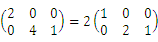
- B.3
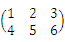 =
=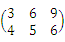
- C.5
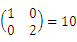
- D.
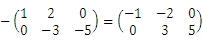
- A.
-
下列矩阵中,是初等矩阵的为( )
- A.
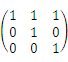
- B.
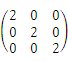
- C.
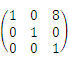
- D.
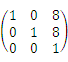
- A.
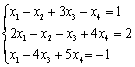 是否有解,有解时求出它的解.
是否有解,有解时求出它的解.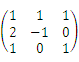 ,B=
,B= ,求:(1)ATB;(2)|ATB|.
,求:(1)ATB;(2)|ATB|.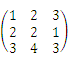 ,B=
,B=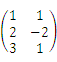 ,B=(1,2,3),则BA= .
,B=(1,2,3),则BA= . 中第4行各元素的代数余子式之和为_________.
中第4行各元素的代数余子式之和为_________.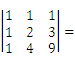 __________.
__________.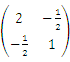
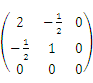
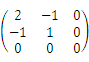
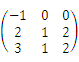 ,则A的对应于特征值λ=0的特征向量为( )
,则A的对应于特征值λ=0的特征向量为( )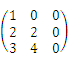 ,那么矩阵A的列向量组的秩为( )
,那么矩阵A的列向量组的秩为( )