线性代数(经管类)2008年10月真题试题及答案解析(04184)
-
已知矩阵A=
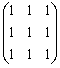 ,求正交矩阵P和对角矩阵Λ,使
,求正交矩阵P和对角矩阵Λ,使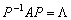 .
. -
设η为非齐次线性方程组Ax=b的一个解,
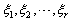 是其导出组Ax=0的一个基础解系.证明
是其导出组Ax=0的一个基础解系.证明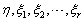 线性无关
线性无关 -
设向量组
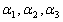 线性无关,令
线性无关,令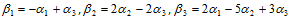 试确定向量组
试确定向量组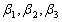 的线性相关性.
的线性相关性. -
已知线性方程组
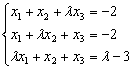 ,
,(1)讨论为何值时,方程组无解、有惟一解、有无穷多个解.
(2)在方程组有无穷多个解时,求出方程组的通解(用一个特解和导出组的基础解系表示).
-
计算行列式D=
 的值
的值 -
已知A=
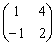 ,B=
,B=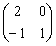 ,C=
,C=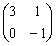 ,矩阵X满足AXB=C,求解X.
,矩阵X满足AXB=C,求解X. -
求向量
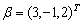 在基
在基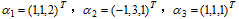 下的坐标,并将β用此基线性表示.
下的坐标,并将β用此基线性表示. -
矩阵A=
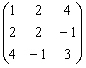 对应的二次型f= .
对应的二次型f= . -
设矩阵A=
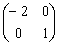 ,则二次型XTAX的规范形是 .
,则二次型XTAX的规范形是 . -
设向量组
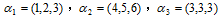 与向量组
与向量组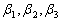 等价,则向量组
等价,则向量组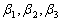 的秩为____.
的秩为____. -
设3阶实对称矩阵A的特征值为
 ,则r(A)= ____.
,则r(A)= ____. -
已知3阶矩阵A的3个特征值为1,2,3,则|A*|=____.
-
设向量
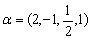 ,则α的长度为____。
,则α的长度为____。 -
已知向量组
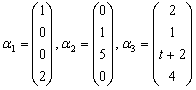 的秩为2,则数t=____.
的秩为2,则数t=____. -
设方程组
 有非零解,则数k=____.
有非零解,则数k=____. -
设矩阵A=
 ,B=
,B= ,则ATB= .
,则ATB= . -
设矩阵A=
 ,则A的特征值为( )
,则A的特征值为( )- A.1,1,0
- B.-1,1,1
- C.1,1,1
- D.1,-1,-1
-
已知行列式
 ,则数a =____.
,则数a =____. -
设A为n(n≥2)阶矩阵,且A2=E,则必有( )
- A.A的行列式等于1
- B.A的逆矩阵等于E
- C.A的秩等于n
- D.A的特征值均为1
-
已知矩阵A与对角矩阵D=
 相似,则A2= ( )
相似,则A2= ( )- A.A
- B.D
- C.E
- D.-E
-
设m×n矩阵A的秩r(A)=n-3(n>3),α,β,γ是齐次线性方程组Ax=0的三个线性无关的解向量,则方程组Ax=0的基础解系为( )
- A.

- B.

- C.

- D.

- A.
-
已知
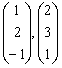 是齐次线性方程组Ax=0的两个解,则矩阵A可为( )
是齐次线性方程组Ax=0的两个解,则矩阵A可为( )- A.(5,-3,-1)
- B.
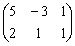
- C.
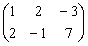
- D.

-
设A是2阶可逆矩阵,则下列矩阵中与A等价的矩阵是( )
- A.
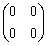
- B.

- C.

- D.

- A.
-
设向量
 下列命题中正确的是( )
下列命题中正确的是( )- A.若α1,α2线性相关,则必有β1,β2线性相关
- B.若α1,α2线性无关,则必有β1,β2线性无关
- C.若β1,β2线性相关,则必有α1,α2线性无关
- D.若β1,β2线性无关,则必有α1,α2线性相关
-
已知矩阵
 ,则AB-BA=( )
,则AB-BA=( )- A.

- B.

- C.

- D.
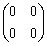
- A.
-
设A、B为n阶方阵,满足A2=B2,则必有( )
- A.A=B
- B.A=-B
- C.|A|=|B|
- D.A2=B2
-
设A为3阶方阵,且
 ,则( )
,则( )- A.-9
- B.-3
- C.-1
- D.9
 ,求正交矩阵P和对角矩阵Λ,使
,求正交矩阵P和对角矩阵Λ,使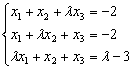 ,
, 的值
的值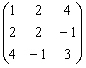 对应的二次型f= .
对应的二次型f= .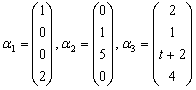 的秩为2,则数t=____.
的秩为2,则数t=____.  ,则A的特征值为( )
,则A的特征值为( ) ,则数a =____.
,则数a =____. 相似,则A2= ( )
相似,则A2= ( )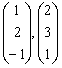 是齐次线性方程组Ax=0的两个解,则矩阵A可为( )
是齐次线性方程组Ax=0的两个解,则矩阵A可为( )