线性代数(经管类)2007年10月真题试题及答案解析(04184)
-
设A是n阶方阵,且
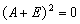 ,证明A可逆.
,证明A可逆. -
给定线性方程组
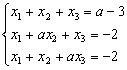 .
.(1)问a为何值时,方程组有无穷多个解;
(2)当方程组有无穷多个解时,求出其通解(用一个特解和导出组的基础解系表示).
-
求矩阵A=
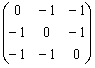 的全部特征值及对应的全部特征向量.
的全部特征值及对应的全部特征向量. -
设向量
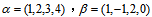 ,求(1)矩阵αTβ;(2)向量α与β的内积(α, β).
,求(1)矩阵αTβ;(2)向量α与β的内积(α, β). -
设2阶矩阵A可逆,且
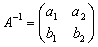 ,对于矩阵
,对于矩阵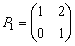 ,
,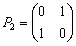 ,令
,令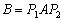 ,求B-1.
,求B-1. -
求向量组
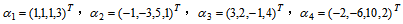 的秩和一个极大线性无关组.
的秩和一个极大线性无关组. -
二次型
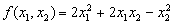 的秩为____.
的秩为____. -
求4阶行列式
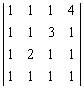 的值.
的值. -
若实对称矩阵A=
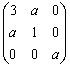 为正定矩阵,则a的取值应满足 .
为正定矩阵,则a的取值应满足 . -
已知3元齐次线性方程组
 有非零解,则a=____.
有非零解,则a=____. -
设A为n阶可逆矩阵,已知A有一个特征值为2,则(2A)-1必有一个特征值为 .
-
设A为m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r,则矩阵B=AC的秩为____.
-
设向量
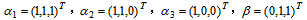 则β由
则β由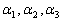 线性表出的表示式为 .
线性表出的表示式为 . -
设向量
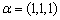 ,则它的单位化向量为 .
,则它的单位化向量为 . -
设3阶矩阵A=
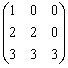 ,则A*A= .
,则A*A= . -
设3阶矩阵A=
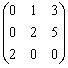 ,则(AT)-1.
,则(AT)-1. -
设A为3阶矩阵,且已知|3A+2E|=0,则A必有一个特征值为( )
- A.-3/2
- B.-2/3
- C.2/3
- D.3/2
-
二次型
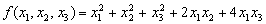 的矩阵为( )
的矩阵为( )- A.
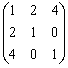
- B.
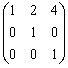
- C.
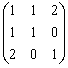
- D.

- A.
-
设矩阵A=
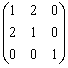 ,B=
,B=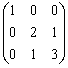 ,则A+2B= .
,则A+2B= . -
设3阶矩阵A与B相似,且已知A的特征值为2,2,3,则|B-1|= ( )
- A.1/12
- B.1/7
- C.7
- D.12
-
设A为m×n矩阵,则齐次线性方程组Ax=0仅有零解的充分必要条件是( )
- A.A的列向量组线性无关
- B.A的列向量组线性相关
- C.A的行向量组线性无关
- D.A的行向量组线性相关
-
已知
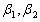 是非齐次线性方程组Ax=b的两个不同的解,
是非齐次线性方程组Ax=b的两个不同的解,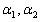 是其导出组Ax=0的一个基础解系,C1,C2为任意常数,则方程组Ax=b的通解可以表为( )
是其导出组Ax=0的一个基础解系,C1,C2为任意常数,则方程组Ax=b的通解可以表为( )- A.
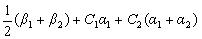
- B.

- C.
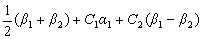
- D.
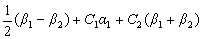
- A.
-
设A为2阶可逆矩阵,且已知
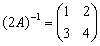 ,则A=( )
,则A=( )- A.2
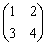
- B.
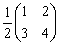
- C.2
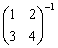
- D.

- A.2
-
设向量组
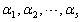 线性相关,则必可推出( )
线性相关,则必可推出( )- A.
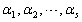 中至少有一个向量为零向量
中至少有一个向量为零向量 - B.
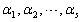 中至少有两个向量成比例
中至少有两个向量成比例 - C.
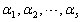 中至少有一个向量可以表示为其余向量的线性组合
中至少有一个向量可以表示为其余向量的线性组合 - D.
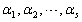 中每一个向量都可以表示为其余向量的线性组合
中每一个向量都可以表示为其余向量的线性组合
- A.
-
设A为3阶方阵,且已知|-2A|=2,则|A|=( )
- A.-1
- B.-1/4
- C.1/4
- D.1
-
设矩阵A,B,C为同阶方阵,则(ABC)T( )
- A.ATBTCT
- B.CTBTAT
- C.CTATBT
- D.ATCTBT
-
设行列式
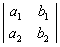 =1,
=1,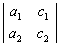 =2,则
=2,则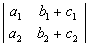 =( )
=( )- A.-3
- B.-1
- C.1
- D.3
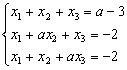 .
.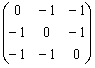 的全部特征值及对应的全部特征向量.
的全部特征值及对应的全部特征向量. 的值.
的值. 为正定矩阵,则a的取值应满足 .
为正定矩阵,则a的取值应满足 . 有非零解,则a=____.
有非零解,则a=____. ,则A*A= .
,则A*A= . ,则(AT)-1.
,则(AT)-1.



 ,B=
,B= ,则A+2B= .
,则A+2B= .