概率论与数理统计(经管类)2014年4月真题
-
设随机变量X~N(0,1),记Y=2X,
求:(1) P{X<-1};(2) P{|X|<1};(3) Y的概率密度。(附:Φ(1)=0.8413)
-
某项经济指标X~N(μ,2),将随机调查的11个地区的该项指标
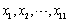 作为样本,算得样本方差S2=3。问可否认为该项指标的方差仍为2?(显著水平=0.05)
作为样本,算得样本方差S2=3。问可否认为该项指标的方差仍为2?(显著水平=0.05)(附:
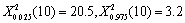 )
) -
有甲、乙两盒,甲盒装有4个白球1个黑球,乙盒装有3个白球2个黑球。从甲盒中任取1个球,放入乙盒中,再从乙盒中任取2个球。求:
(1) 从乙盒中取出的是2个黑球的概率;
(2) 己知从乙盒中取出的是2个黑球,问从甲盒中取出的是白球的概率。
-
设二维随机变量(X,Y)的分布律为
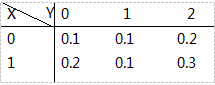
求:(1) E(Y),D(X);(2) E(X+Y)。
-
某假设检验的拒绝域为W,当原假设H0成立时,样本值(
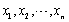 )落入W的概率为0.1,则犯第一类错误的概率为________。
)落入W的概率为0.1,则犯第一类错误的概率为________。 -
设二维随机变量(X,Y)的概率密度为
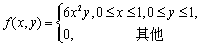
求:(1) (X,Y)关于X的边缘概率密度fx(x);(2) P{X>Y}。
-
设总体X~N(μ,16),μ未知,
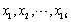 为来自该总体的样本,
为来自该总体的样本, 为样本均值,
为样本均值,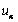 为标准正态分布的上侧α分位数。当μ的置信区间是
为标准正态分布的上侧α分位数。当μ的置信区间是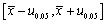 时,则置信度为________。
时,则置信度为________。 -
设样本的频数分布为
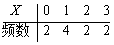 ,则样本均值=________。
,则样本均值=________。 -
设总体X~N(0,1),
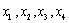 为来自总体X的样本,则统计量
为来自总体X的样本,则统计量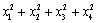 ~________。
~________。 -
设随机变量X~B(100,0.2),Φ(x)为标准正态分布函数,Φ(2.5)=0.9938,应用中心极限定理,可得P{20≤X≤30}≈________。
-
设X,Y为随机变量,且E(X)=E(Y)=1,D(X)=D(Y)=5,
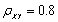 ,则E(XY)=________。
,则E(XY)=________。 -
设随机变量X与Y相互独立,且X~N (0,1),Y~N(-1,1),记Z=X-Y,则Z~________。
-
设随机变量X服从参数为2的指数分布,则E(X2)=_________。
-
设二维随机变量(X,Y)的分布律为

则常数a=________。
-
设随机变量X的概率密度为
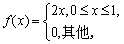 ,则
,则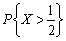 =________。
=________。 -
已知随机变量X~N(4,9),
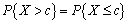 ,则常数c=________。
,则常数c=________。 -
设随机变量X服从区间[1,5]上的均匀分布,F(x)为X的分布函数,当1≤x≤5时,F(x)=________。
-
设A,B为对立事件,则
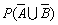 =________。
=________。 -
设随机事件A与B相互独立,P(A)=0.3,P(B)=0.4,则P(A-B)=________。
-
设A、B为随机事件,
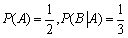 ,则P(AB)=________。
,则P(AB)=________。 -
设一元线性回归模型为
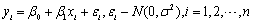 ,则E(yi)=( )
,则E(yi)=( )- A.
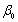
- B.
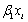
- C.
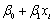
- D.

- A.
-
设
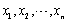 为来自正态总体N(μ,1)的样本,
为来自正态总体N(μ,1)的样本,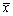 为样本均值,s2为样本方差。检验假设
为样本均值,s2为样本方差。检验假设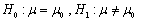 ,则采用的检验统计量应为()
,则采用的检验统计量应为()- A.
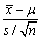
- B.
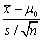
- C.
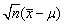
- D.
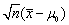
- A.
-
设
 为来自某总体的样本,
为来自某总体的样本,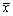 为样本均值,则
为样本均值,则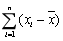 =( )
=( )- A.
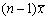
- B.0
- C.
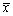
- D.
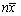
- A.
-
设总体X的方差为σ2,
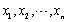 为来自该总体的样本,
为来自该总体的样本,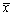 为样本均值,则参数σ2的无偏估计为()
为样本均值,则参数σ2的无偏估计为()- A.
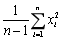
- B.
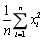
- C.
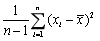
- D.
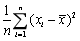
- A.
-
设随机变量X服从参数为2的泊松分布,则D(9-2X)=( )
- A.1
- B.4
- C.5
- D.8
-
设(X,Y)为二维随机变量,则与Cov(X,Y)=0不等价的是( )
- A.X与Y相互独立
- B.D(X-Y)=D(X)+D(Y)
- C.E(XY)=E(X)E(Y)
- D.D(X+Y)=D(X)+D(Y)
-
设X为随机变量,E(x)=0.1,D(X)=0.01,则由切比雪夫不等式可得( )
- A.
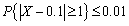
- B.
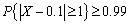
- C.
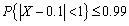
- D.
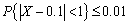
- A.
-
设二维随机变量(X,Y)的概率密度为
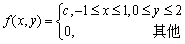 ,则常数c=( )
,则常数c=( )- A.1/4
- B.1/2
- C.2
- D.4
-
设随机变量X的分布律为
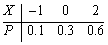 ,F(x)为X的分布函数,则F(0)=( )
,F(x)为X的分布函数,则F(0)=( )- A.0.1
- B.0.3
- C.0.4
- D.0.6
-
掷一颗骰子,观察出现的点数。A表示“出现3点”,B表示“出现偶数点”,则( )
- A.
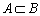
- B.
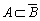
- C.
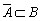
- D.
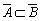
- A.


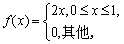 ,则
,则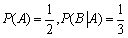 ,则P(AB)=________。
,则P(AB)=________。