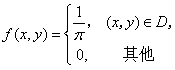概率论与数理统计(经管类)2012年10月真题
-
某种产品用自动包装机包装,每袋重量X~N(500,22)(单位:g),生产过程中包装机工作是否正常要进行随机检验。某天开工后抽取了9袋产品,测得样本均值
 。问:当方差不变时,这天包装机工作是否正常(α=0.05)?(附:u0.025=1.96)
。问:当方差不变时,这天包装机工作是否正常(α=0.05)?(附:u0.025=1.96) -
某次抽样结果表明,考生的数学成绩(百分制)近似地服从正态分布N(75,σ2),已知85分以上的考生数占考生总数的5%,试求考生成绩在65分至85分之间的概率。
-
设随机变量X服从区间[0,1]上的均匀分布,Y服从参数为1的指数分布,且X与Y相互独立。求:
(1)X及Y的概率密度;
(2)(X,Y)的概率密度;
(3)P{X>Y}。
-
已知二维随机变量(X,Y)的分布律

求:(1)X和Y的分布律;(2)Cov(X,Y)
-
一批零件由两台车床同时加工,第一台车床加工的零件数比第二台多一倍。第一台车床出现不合格品的概率是0.03,第二台出现不合格品的概率是0.06。
求:(1)求任取一个零件是合格品的概率;
(2)如果取出的零件是不合格品,求它是由第二台车床加工的概率。
-
设总体X~N(μ,σ2),且σ2未知,
 为来自总体的样本,
为来自总体的样本, 和S2分别是样本均值和样本方差,则检验假设
和S2分别是样本均值和样本方差,则检验假设 采用的统计量表达式为________。
采用的统计量表达式为________。 -
设
 是来自总体B(20,p)的样本,则p的矩估计
是来自总体B(20,p)的样本,则p的矩估计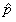 =________。
=________。 -
设总体服从正态分布N(μ,1),从中抽取容量为16的样本,
 是标准正态分布的上侧α分位数,则μ的置信度为0.96的置信区间长度是________。
是标准正态分布的上侧α分位数,则μ的置信度为0.96的置信区间长度是________。 -
设
 是来自总体P(λ)的样本,
是来自总体P(λ)的样本, 是样本均值,则D(
是样本均值,则D( )=________。
)=________。 -
设m为n次独立重复试验中事件A发生的次数,p为事件A的概率,则对任意正数ε,有
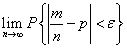 =________。
=________。 -
设随机变量X~U(-1,3),则D(2X-3)=________。
-
设二维随机变量(X,Y)的分布律

则E(X2+Y2)=________。
-
设随机变量X服从区间[2,θ]上的均匀分布,且概率密度f(x)=
 ,则θ=________。
,则θ=________。 -
设二维随机变量(X,Y)的分布律
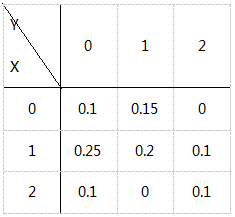
则P{X=Y}=________。
-
设二维随机变量(X,Y)~N(0,0,1,4,0),则X的概率密度fX(x)=________。
-
设随机变量X的分布律为
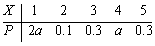 ,则a=________。
,则a=________。 -
设随机变量X~N(1,22),则P{-1≤X≤3}=________。(附:Ф(1)=0.8413)
-
设甲、乙两人独立地向同一目标射击,甲、乙击中目标的概率分别为0.8,0.5,则甲、乙两人同时击中目标的概率为________。
-
设A,B为两事件,且P(A)=P(B)=1/3,P(A|B)=1/6,则
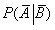 =________。
=________。 -
已知事件A,B满足P(AB)=P(

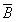 ),若P(A)=0.2,则P(B)=________。
),若P(A)=0.2,则P(B)=________。 -
在假设检验中,H0为原假设,H1为备择假设,则第一类错误是()
- A.H1成立,拒绝H0
- B.H0成立,拒绝H0
- C.H1成立,拒绝H1
- D.H0成立,拒绝H1
-
设一元线性回归模型:
 且各
且各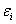 相互独立.
相互独立.
- A.
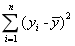
- B.
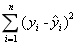
- C.
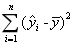
- D.
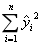
- A.
-
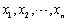 设为来自总体N(μ,σ2)的样本,μ,σ2是未知参数,则下列样本函数为统计量的是()
设为来自总体N(μ,σ2)的样本,μ,σ2是未知参数,则下列样本函数为统计量的是()- A.
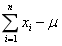
- B.
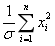
- C.
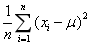
- D.
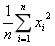
- A.
-
对总体参数进行区间估计,则下列结论正确的是()
- A.置信度越大,置信区间越长
- B.置信度越大,置信区间越短
- C.置信度越小,置信区间越长
- D.置信度大小与置信区间长度无关
-
设二维随机变量(X,Y)的分布律
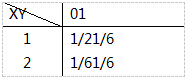
则D(3X)=()
- A.2/9
- B.2
- C.4
- D.6
-
设X1,X2,…,Xn…为相互独立同分布的随机变量序列,且E(X1)=0,D(X1)=1,则
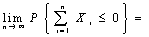 ()
()- A.0
- B.0.25
- C.0.5
- D.1
-
设F(x)为随机变量X的分布函数,则有()
- A.F(-∞)=0,F(+∞)=0
- B.F(-∞)=1,F(+∞)=0
- C.F(-∞)=0,F(+∞)=1
- D.F(-∞)=1,F(+∞)=1
-
设二维随机变量(X,Y)服从区域D:x2+y2≤1上的均匀分布,则(X,Y)的概率密度为()
- A.f(x,y)=1
- B.
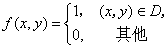
- C.f(x,y)=1/π
- D.
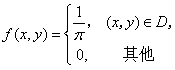
-
设随机变量X服从参数为2的指数分布,则E(2X-1)=()
- A.0
- B.1
- C.3
- D.4
-
已知事件A,B,A∪B的概率分别为0.5,0.4,0.6,则
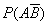 =()
=()- A.0.1
- B.0.2
- C.0.3
- D.0.5

 采用的统计量表达式为________。
采用的统计量表达式为________。
 ,则θ=________。
,则θ=________。