2013年专升本（高数）真题

求微分方程y"-2y+y=e^-x的通解。

计算xy²dxdy，其中积分区域D由直线y=x，x=1及x轴围成。

求由曲线y=x²(x≥0)，直线y=1及y轴围成的平面图形的面积。

设z=xy²+eycosx，求

求

求函数f(x)=x³-3x+5的极大值与极小值。

求

设函数f(x)=在x=1处连续，求a。

设区域D={(x，y)|x²+y²≤4}，则=________。

过坐标原点且与平面2x-y+z+1=0平行的平面方程为________。

设z=xy，则dz=________。

幂级数的收敛半径R=________。

∫₀¹2e^xdx=________。

∫cos(x+2)dx=________。

设y=5+lnx，则dy=________。

设y=2e^x-1，则y"=________。

设y=(x+3)²，则y=________。

=________。

微分方程(y)²=x的阶数为(  )

• A.1
• B.2
• C.3
• D.4

(  )

• A.
• B.0
• C.    
• D.1

设z=3x²+5y，则(  )

• A.5y
• B.3x
• C.6x
• D.6x+5

设y=3+sinx，则y=(  )

• A.-cosx
• B.cosx
• C.1-cosx
• D.1+cosx

(  )

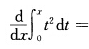• A.x²
• B.2x²
• C.x
• D.2x

(  )

• A.
• B.-3ln|x|+C
• C.    
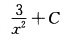
• D.3ln|x|+C

设y=-2e^x，则y=( )

• A．e^x
• B．2e^x
• C．-e^x
• D．-2e^x

设y=2x³，则dy=( )

• A．2x²dx
• B．6x²dx
• C．3x²dx
• D．x²dx

设y=3+x²，则y=( )

• A．2x
• B．3+2x
• C．3
• D．x²