2016广东高职高考数学试卷真题及答案

设椭圆 C :x^2/a^2 +y^2 =1 的焦点在 x轴上，其离心率为

（1）求椭圆 C的方程； 

（2）求椭圆 C上的点到直线 l : y=x+4 的距离的最小值和最大值

已知数列{an}的前n项和{Sn}满足an+sn=1(n∈N*) ． 

（1）求{an}的通项公式； 

（2）设，求数列{bn}的前n项和Tn ．

在?ABC中 ，已知a=1,b=2, cosC=-1/4 

（1）求?ABC 的周长； 

（2）求 sin(A+ C ) 的值．

如图所示，在平面直角坐标系 xoy中,已知点 A （-2,0）和 B (8,0)，以AB为直径作半圆交 y轴于点M，点P为半圆的圆心，以 AB为边作正方形 ABCD，CD交y轴于点N，连接CM和MP． 

（1）求点C，P和M的坐标； 

（2）求四边形 BCMP的面积S．

已知直角三角形的顶点 A(-4,4)，B(-1,7)和 C(2,4)，则该三角形外接圆的方程是 ．

已知 sin( π/6-a) = -1/2 cosa，则 tan a=．

在?ABC 中，若 AB =2,则． 

某高中学校三个年级共有学生 2000名，若在全校学生中随机抽取一名学生，抽到高二年级女生的概率为 0.19，则高二年级的女生人数为 ．

同时抛三枚硬币，恰有两枚硬币正面朝上的概率是（ ）

• A.1/8
• B.1/4
• C.3/8
• D.5/8

已知{an} 为等差数列，且a4+ a8 +a10 =50 ，则a2+ 2 a10=．

已知直线 l 的倾斜角为π/4，在 y 轴上的截距为 2，则 l 的方程是（ ）

• A.Y+x-2=0
• B.Y+x+2=0
• C.Y-x-2=0
• D.Y-x+2=0

若样本数据 3,2, x ,5 的均值为3，则该样本的方差是（ ）

• A.2
• B.1.5
• C.2.5
• D.6

设三点A(1,2)B(-1,3)和C(x-1,5) ，若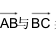共线，则 x =（ ）

• A.-4
• B.-1
• C.1
• D.4

抛物线x^2=4y的准线方程是（ ）

• A.Y=-1
• B.Y=1
• C.x=-1
• D.X=1

在等比数列{an} 中，已知a3=7,a6=56，则该等比数列的公比是（ ）

• A.2
• B.3
• C.4
• D.8

函数y=(sin2x-cos2x)^2的中最小正周期是（ ）

• A.Π/2
• B.Π
• C.2Π
• D.4Π

已知 f(x) 为偶函数，且 y=f(x)的图像经过点 (2 , -5 ) ，则下列等式恒成立的是（ ）

• A.f(-5)=2
• B.f(-5)=-2
• C.f(-2)=5
• D.f(-2)=-5

设向量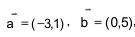则 ∣a- b∣=（ ）

• A.1
• B.3
• C.4
• D.5

函数 y=cos( π/2 - x )在区间[π/3, 5π/6]上的最大值是（ ）

• A.1/2
• B.√2/2
• C.√3/2
• D.1

若a,b为实数，则 " b=3" 是a( b-3)= 0的（ ）

• A.充分非必要条件
• B.必要非充分条件
• C.充分必要条件
• D.非充分必要条件

不等式 x^2-5x-6≤0 的解集是（ ）

• A.{x∣-2≤x≤3}
• B.{x∣-1≤x≤6}
• C.{x∣-6≤x≤1}
• D.{x∣x≤-1或x≥6}

下列函数在其定义域内单调递增的是（ ）

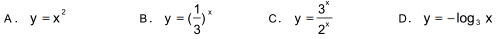
• A.A
• B.B
• C.C
• D.D

函数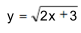的定义域是（ ）

• A.（-∞,+∞）
• B.[-3/2,+∞)
• C.(-∞, -3/2]
• D.( 0,+∞)

设集合 A={2,3, a}, B={1,4}, 且A ∩B ={4 }，则a = （ ）

• A.1
• B.2
• C.3
• D.4