高职单招考试数学考前押题试卷附答案（一）

(1) 求该直线l的方程;

(2) 求圆心该直线上且与两坐标轴相切的圆的标准方程.

己知正方体ABCD-A₁B₁C₁D₁，证明：直线AC₁与直线A₁D₁所成角的余弦值为.

己知a= (-1，2)，b= (-2，1)，证明：cos〈a，b〉=4/5.

近年来，某市为了促进生活垃圾的分类处理，将生活垃圾分为“厨余垃圾”、“可回收垃圾”、“有害垃圾” 和“其他垃圾”等四类，并分别垛置了相应的垃圾箱，为调查居民生活垃圾的正确分类投放情况，现随机抽取了 该市四类垃圾箱总计100吨生活垃圾，数据统计如下(单位：吨)：

(1) 试估计“可回收垃圾”投放正确的概率;

(2) 试估计生活垃圾投放错误的概率。

已知函数y=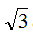cos2x + 3sin2x，x ∈ R求:

(1) 函数的值域;

(2) 函数的最小正周期。

在等比数列{a_n}中,a₅=4，a₇=6，则S₉=     。

有四个数，前三个数成等差数列，公差为10，后三个数成等比数列，公比为3，求这四个数.

某机电班共有50名学生，任选一人是男生的概率为0.4,则这个班的男生共有名      。

若f(x-1) = x²-2x + 3,则f(x)=      。

若长方体的长、宽、高分别为1, 2, 3,则其对角线长为     。

计算： log₂16 + cosπ + 27^1/3=      。

10lg2 =      。

过点(1，-1),且与直线3x-2y+1=0垂直的直线方程为     。

若函数f(x) = kx + b,在R上是增函数，则( )

• A.k>0
• B.k<0
• C.b<0
• D.b>0

如图所示，某人向圆内投镖，如果他每次都投入圆内，那么他投中正方形区域的概率为    。

己知向量a= (2，1)，b=(-1，2)，则a,b之间的位置关系为( )

• A.平行
• B.不平行也不垂直
• C.垂直
• D.以上都不对

设函数f(x) = x²+1，则f(x)是( )

• A.奇函数
• B.偶函数
• C.非奇非偶函数
• D.既是奇函数又是偶函数

在△ABC中，“x²=1” 是 “x =1” 的( )

• A.充分不必要条件
• B.必要不充分条件
• C.充分必要条件
• D.既不充分也不必要条件

在正方体ABCD-A₁B₁C₁D₁中，二面角D₁-AB-D的大小是( )

• A.30°
• B.60°
• C.45°
• D.90°

若a^0.60.4，则a的取值范围为（ ）

• A.a>1
• B.0
• C.a>0
• D.无法确定

对于数列0,0,0,...,0,...,下列表述正确的是()

• A.是等比但不是等差数列
• B.既是等差又是等比数列
• C.既不是等差又不是等比数列
• D.是等差但不是等比数列

己知|x-3|

• A.-6
• B.6
• C.±6
• D.0

A ≠ф是A∩B=ф的( )

• A.充分条件
• B.必要条件
• C.充要条件
• D.无法确定

若f(x)=a²+bx(ab≠0)，且f(2) = f(3)，则f(5)等于( )

• A.1
• B.-1
• C.0
• D.2