2012年考研(数学一)真题试卷
-
设随机变量X与Y相互独立且分别服从正态分布N(μ,δ2)与N(μ,2δ2),其中δ是未知参数且δ>0.设Z=X-Y
(1)求x的概率密度fZ(z);
(2)设Z1,Z2,…,Zn为来自总体z的简单随机样本,求δ2的最大似然估计量
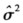 ;
;(3)证明
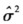 为δ2的无偏估计量.
为δ2的无偏估计量. -
设二维离散型随机变量X、Y的概率分布为
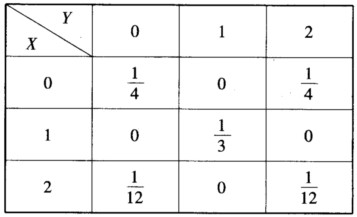
(I)求P{X=2Y};
(Ⅱ)求Cov(X-Y,Y)与ρXY.
-
已知
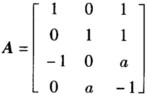 ,二次型f(x1,x2,x3)=xT(ATA)x的秩为2.
,二次型f(x1,x2,x3)=xT(ATA)x的秩为2.(1)求实数a的值;
(2)求正交变换x=Qy将f化为标准形.
-
已知L是第一象限中从点(0,0)沿圆周x2+y2=2x到点(2,0),再沿圆周x2+y2=4到点(0,2)的曲线段,计算曲线积分
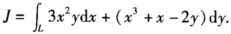
-
已知
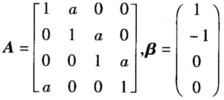
(1)计算行列式|A|.
(2)当实数α为何值时,方程组Ax=β有无穷多解,并求其通解.
-
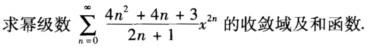
-
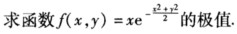
-
已知曲线
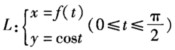 ,其中函数f(t)具有连续导数,且f(0)=0,fˊ(t)>0,(0<t<π/2),若曲线L的切线与x轴的交点到切点的距离值恒为1,求函数f(t)的表达式,并求此曲线L与x轴与y轴无边界的区域的面积.
,其中函数f(t)具有连续导数,且f(0)=0,fˊ(t)>0,(0<t<π/2),若曲线L的切线与x轴的交点到切点的距离值恒为1,求函数f(t)的表达式,并求此曲线L与x轴与y轴无边界的区域的面积. -
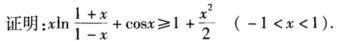
-
设∑={(x,y,z)|x+y+z=1,x≥0,y≥0,z≥0},则
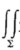 y2dx=________.
y2dx=________. -
设A、B、C是随机事件,A与C互不相容,P(AB)=1/2,P(C)=1/3,则P(AB|C ̄)=________.
-
设X为三维单位列向量,E为三阶单位矩阵,则矩阵E-XXT的秩为_________.
-

-
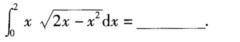
-
设随机变量X与Y相互独立,且分别服从参数为1与参数为4的指数分布,则P|x<y|=( ).
- A.1/5
- B.1/3
- C.2/5
- D.4/5
-
若函数f(x)满足方程f〞(x)+fˊ(x)-2f(x)=0及fˊ(x)+f(x)=2ex,则f(x)=__________.
-
将长度为1 m的木棒随机地截成两段,则两段长度的相关系数为( ).
- A.1
- B.1/2
- C.﹣1/2
- D.﹣1
-
设
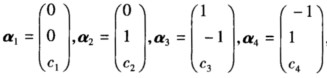 ,其中c1,c2,c3,c4为任意常数,则下列向量组线性相关的为( ).
,其中c1,c2,c3,c4为任意常数,则下列向量组线性相关的为( ).- A.α1,α2,α3
- B.α1,α2,α4
- C.α1,α3,α4
- D.α2,α3,α4
-
设A为3阶矩阵,P为3阶可逆矩阵,且
 若P=(α1,α2,α3),Q=(α1+α2,α2,α3),则Q-1AQ=( ).
若P=(α1,α2,α3),Q=(α1+α2,α2,α3),则Q-1AQ=( ).
- A.
- B.
- C.
- D.
-
如果函数f(x,y)在(0,0)处连续,那么下列命题正确的是( ).

- A.
- B.
- C.
- D.
-
设
 (k=1,2,3),则有( ).
(k=1,2,3),则有( ).- A.I1<I2<13
- B.I3<I2<I1
- C.I2<I3<I1
- D.I2<I1<I3
-
设函数f(x)=(ex-1)(e2x-2)…(enx-n),其中n为正整数,则fˊ(0)=( ).
- A.(-1)n-1(n-1)!
- B.(-1)n(n-1)!
- C.(-1)n-1n!
- D.(-1)nn!
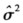 ;
;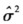 为δ2的无偏估计量.
为δ2的无偏估计量.
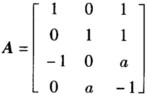 ,二次型f(x1,x2,x3)=xT(ATA)x的秩为2.
,二次型f(x1,x2,x3)=xT(ATA)x的秩为2.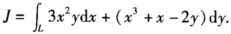
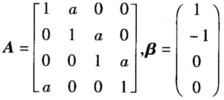
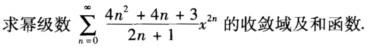
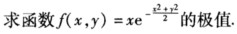
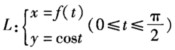 ,其中函数f(t)具有连续导数,且f(0)=0,fˊ(t)>0,(0<t<π/2),若曲线L的切线与x轴的交点到切点的距离值恒为1,求函数f(t)的表达式,并求此曲线L与x轴与y轴无边界的区域的面积.
,其中函数f(t)具有连续导数,且f(0)=0,fˊ(t)>0,(0<t<π/2),若曲线L的切线与x轴的交点到切点的距离值恒为1,求函数f(t)的表达式,并求此曲线L与x轴与y轴无边界的区域的面积.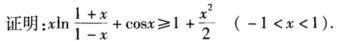
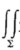 y2dx=________.
y2dx=________.
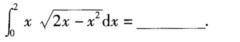
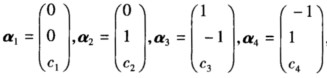 ,其中c1,c2,c3,c4为任意常数,则下列向量组线性相关的为( ).
,其中c1,c2,c3,c4为任意常数,则下列向量组线性相关的为( ). 若P=(α1,α2,α3),Q=(α1+α2,α2,α3),则Q-1AQ=( ).
若P=(α1,α2,α3),Q=(α1+α2,α2,α3),则Q-1AQ=( ).

 (k=1,2,3),则有( ).
(k=1,2,3),则有( ).