2013年1月MBA联考综合能力(数学)真题试卷
-
方程|x+1|+|x+3|+|x一5|=9存在唯一解. (1)|x—2|≤3. (2)|x—2|≥2.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
设直线y=x+b分别在第一和第三象限与曲线y=
 相交于点A,点B,则能确定b的值. (1)已知以AB为对角线的正方形的面积. (2)点A的横坐标小于纵坐标.
相交于点A,点B,则能确定b的值. (1)已知以AB为对角线的正方形的面积. (2)点A的横坐标小于纵坐标.- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
设{an}是等比数列.则a2=2. (1)a1+a3=5. (2)a1a3=4.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
甲、乙两人以不同的速度在环形跑道上跑步,甲比乙快.则乙跑一圈需要6分钟. (1)甲、乙相向而行,每隔2分钟相遇一次. (2)甲、乙同向而行,每隔6分钟相遇一次.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
设a,b为常数.则关于z的二次方程(a2+1)x2+2(a+b)x+b2+1=0具有重实根. (1)a,1,b成等差数列. (2)a,1,b成等比数列.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
已知f(x,y)=x2一y2一x+y+1.则f(x,y)=1. (1)x—y. (2)x+y=1.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
设a是整数.则a=2. (1)二次方程ax2+8x+6=0有实根. (2)二次方程x2+5ax+9=0有实根.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
已知圆A:x2+y2+4x+2y+1=0.则圆B和圆A相切. (1)圆B:x2+y2一2x一6y+1=0. (2)圆B:x2+y2一6x=0.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
产品出厂前,需要在外包装上打印某些标志.甲、乙两人一起每小时可完成600件.则可以确定甲每小时完成多少件. (1)乙的打件速度是甲的打件速度的
 . (2)乙工作5小时可以完成1 000件.
. (2)乙工作5小时可以完成1 000件.- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
m2n2一1能被2整除. (1)m是奇数. (2)n是奇数.
- A.条件(1)充分,但条件(2)不充分.
- B.条件(2)充分,但条件(1)不充分.
- C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
- D.条件(1)充分,条件(2)也充分.
- E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.
-
某单位在甲、乙两个仓库中分别存在着30吨和50吨货物,现要将这批货物转运到A,B两地存放,A,B两地的存放量都是40吨.甲、乙两个仓库到A,B两地的距离(单位:km)如表1所示,甲、乙两个仓库运送到A,B两地的货物重量如表2所示.若每吨货物每km的运费是1元,则下列调运方案中总运费最少的是( ).

- A.x=30,y=10,u=0,v=40
- B.x=0,y=40,u=30,v=10
- C.x=10,y=30,u=20,v=20
- D.x=20,y=20,u=10,v=30
- E.x=15,y=25,u=15,v=25
-
将一个白木质的正方体的六个表面都涂上红漆,再将它锯成64个小正方体.从中任取3个,其中至少有1个三面是红漆的小正方体的概率是( ).
- A.0.665
- B.0.578
- C.0.563
- D.0.482
- E.0.335
-
福彩中心发行彩票的目的是为了筹措资金资助福利事业.现在福彩中心准备发行一种面值为5元的福利彩票刮刮卡,方案设计如下:(1)该福利彩票的中奖率为50%;(2)每张中奖彩票的中奖奖金有5元和50元两种.假设购买一张彩票获得50元奖金的概率为p,且福彩中心筹得资金不少于发行彩票面值总和的32%,则( ).
- A.p≤0.005
- B.p≤0.01
- C.p≤0.01 5
- D.p≤0.02
- E.p≤0.025
-
在某次比赛中有6名选手进入决赛.若决赛设有1个一等奖,2个二等奖,3个三等奖,则可能的结果共有( )种.
- A.16
- B.30
- C.45
- D.60
- E.1 20
-
甲、乙、丙三个容器中装有盐水.现将甲容器中盐水的
 倒入乙容器,摇匀后将乙容器中盐水的
倒入乙容器,摇匀后将乙容器中盐水的 倒入丙容器,摇匀后再将丙容器中盐水的
倒入丙容器,摇匀后再将丙容器中盐水的 倒回甲容器,此时甲、乙、丙三个容器中盐水的含盐量都是9 kg.则甲容器中原来的盐水含盐量是( )kg.
倒回甲容器,此时甲、乙、丙三个容器中盐水的含盐量都是9 kg.则甲容器中原来的盐水含盐量是( )kg.- A.13
- B.12.5
- C.12
- D.10
- E.9.5
-
如图3所示,在正方形ABCD中,弧AOC是四分之一圆周,EF∥AD.若DF=a,CF=b,则阴影部分的面积为( ).

- A.

- B.ab
- C.2ab
- D.b2一a2
- E.(b一a)2
- A.
-
设数列{an}满足:a1=1,an+1=ann+
 (n≥1),则a100=( ).
(n≥1),则a100=( ).- A.1 650
- B.1 651
- C.

- D.3 300
- E.3 301
-
图2是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.此人停留期间空气质量都是优良的概率为( ).
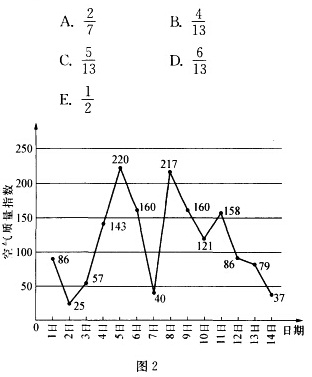
- A.
- B.
- C.
- D.
- E.
-
老王上午8:00骑自行车离家去办公楼开会.若每min骑行150 m,则他会迟到5 min;若每min骑行210 m,则他会提前5 min.会议开始的时间是( ).
- A.8:20
- B.8:30
- C.8:45
- D.9:00
- E.9:10
-
如图1所示,AB=AC=5,BC=6,E是BC的中点,EF⊥AC,则EF=( ).

- A.1.2
- B.2
- C.2.2
- D.2.4
- E.2.5
-
某物流公司将一批货物的60%送到了甲商场,100件送到了乙商场,其余的都送到了丙商场.若送到甲、丙两商场的货物数量之比为7:3,则该批货物共有( )件.
- A.700
- B.800
- C.900
- D.1 000
- E.1 100
-
不等式
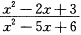 ≥0的解是( ).
≥0的解是( ).- A.(2,3)
- B.(一∞,2]
- C.[3,+∞)
- D.(一∞,2]∪[3,+∞)
- E.(一∞,2)∪(3,+∞)
-
如果a,b,c的算术平均值等于13,且a:b:c=
 ,那么c=( ).
,那么c=( ).- A.7
- B.8
- C.9
- D.12
- E.18
-
某公司今年第一季度和第二季度的产值分别比去年同期增长了11%和9%,且这两个季度产值的同比绝对增加量相等.该公司今年上半年的产值同比增长了( ).
- A.9.5%
- B.9.9%
- C.10%
- D.10.5%
- E.10.9%
-
某学校高一年级男生人数占该年级学生人数的40%.在一次考试中,男、女生的平均分数分别为75分和80分,则这次考试高一年级学生的平均分数为( ).
- A.76
- B.77
- C.77.5
- D.78
- E.79
 相交于点A,点B,则能确定b的值. (1)已知以AB为对角线的正方形的面积. (2)点A的横坐标小于纵坐标.
相交于点A,点B,则能确定b的值. (1)已知以AB为对角线的正方形的面积. (2)点A的横坐标小于纵坐标. . (2)乙工作5小时可以完成1 000件.
. (2)乙工作5小时可以完成1 000件.
 倒入乙容器,摇匀后将乙容器中盐水的
倒入乙容器,摇匀后将乙容器中盐水的 倒入丙容器,摇匀后再将丙容器中盐水的
倒入丙容器,摇匀后再将丙容器中盐水的 倒回甲容器,此时甲、乙、丙三个容器中盐水的含盐量都是9 kg.则甲容器中原来的盐水含盐量是( )kg.
倒回甲容器,此时甲、乙、丙三个容器中盐水的含盐量都是9 kg.则甲容器中原来的盐水含盐量是( )kg.

 (n≥1),则a100=( ).
(n≥1),则a100=( ).


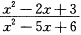 ≥0的解是( ).
≥0的解是( ). ,那么c=( ).
,那么c=( ).