阅读以下说明和c++代码，将应填入(n)处的字句写在对应栏内。

 【说明】

 本程序将两个从小到大的有序链表合成一个新的从小到大的有序链表。链表的每一项由类 Node描述，而链表由List描述，类List的成员函数有以下几个：

 creatList(): 创建从小到大的有序链表。

 multiplyList(List L1, Llst L2): 将链表L1和链表L2合并。

 print(): 打印链表。

 【C++代码】

 #include ＜iostream＞

 using namespace std;

 class List;

 class Node{

    friend class List;

 public:

    Node(int data){

       (1);

    }

 private:

    int data;

    Node *next;

 };

 class List{

 public：

    List(){list=NULL;}

    void multiplyList(List L1, List L2);

    void creatList();

    void print();

 private:

    Node *list;

 };

 void List::creatList()

 {

    Node *p, *u, *pre;

    int dara;

    list=NULL;

    wbile(1){

       cout＜＜"输入链表的一项: (小于零，结束链表) "＜＜endl;

       cin＞＞data;

       if(dara＜0)break;//小于零，结束输入

       p=list;

       while(p !=NULL && dara＞p-＞data){//查找插入点

         pre=p;

         p=p-＞next;

       }

       u=(2);

       if(p==list)list=u;

       else pre-＞next=u;

       (3);

    }

 }

 void List::multiplyList(List L1, List L2)

 {

   Node *pL1, *pL2, *pL, *u;

   list = NULL;

   pL1 = L1.list;

   pL2 = L2.11st;

   while(pL1 != NULL && pL2 != NULL){

      if(pL1-＞data ＜ pL2-＞data){

         u = new Node(pL1-＞data);

         pL1 = pL1-＞next;

      }else{

         u = new Node(pL2-＞data);

         pL2 = pL2-＞next;

      }

      if(list == NULL){

         list =(4);

      }else{

         pL-＞next=u;

         pL=u;

      }

   }

   pL1 = (pL1 != NULL)? pL1:pL2;

   while(pL1 != NULL){

      u=(5);

      pL1 = pL1-＞next;

      if(list == NULL){

        list=pL=u;

      }else{

        pL-＞next=u;

        pL=u;

      }

   }

 }

 void List::print()

 {

    Node *p;

    p = list;

    while(p !=NULL){

      cout＜＜p-＞data＜＜"\t";

      p=p-＞next;

&

阅读以下说明和c++代码，将应填入(n)处的字句写在对应栏内。

 【说明】

 本程序将两个从小到大的有序链表合成一个新的从小到大的有序链表。链表的每一项由类 Node描述，而链表由List描述，类List的成员函数有以下几个：

 creatList(): 创建从小到大的有序链表。

 multiplyList(List L1, Llst L2): 将链表L1和链表L2合并。

 print(): 打印链表。

 【C++代码】

 #include ＜iostream＞

 using namespace std;

 class List;

 class Node{

    friend class List;

 public:

    Node(int data){

       (1);

    }

 private:

    int data;

    Node *next;

 };

 class List{

 public：

    List(){list=NULL;}

    void multiplyList(List L1, List L2);

    void creatList();

    void print();

 private:

    Node *list;

 };

 void List::creatList()

 {

    Node *p, *u, *pre;

    int dara;

    list=NULL;

    wbile(1){

       cout＜＜"输入链表的一项: (小于零，结束链表) "＜＜endl;

       cin＞＞data;

       if(dara＜0)break;//小于零，结束输入

       p=list;

       while(p !=NULL && dara＞p-＞data){//查找插入点

         pre=p;

         p=p-＞next;

       }

       u=(2);

       if(p==list)list=u;

       else pre-＞next=u;

       (3);

    }

 }

 void List::multiplyList(List L1, List L2)

 {

   Node *pL1, *pL2, *pL, *u;

   list = NULL;

   pL1 = L1.list;

   pL2 = L2.11st;

   while(pL1 != NULL && pL2 != NULL){

      if(pL1-＞data ＜ pL2-＞data){

         u = new Node(pL1-＞data);

         pL1 = pL1-＞next;

      }else{

         u = new Node(pL2-＞data);

         pL2 = pL2-＞next;

      }

      if(list == NULL){

         list =(4);

      }else{

         pL-＞next=u;

         pL=u;

      }

   }

   pL1 = (pL1 != NULL)? pL1:pL2;

   while(pL1 != NULL){

      u=(5);

      pL1 = pL1-＞next;

      if(list == NULL){

        list=pL=u;

      }else{

        pL-＞next=u;

        pL=u;

      }

   }

 }

 void List::print()

 {

    Node *p;

    p = list;

    while(p !=NULL){

      cout＜＜p-＞data＜＜"\t";

      p=p-＞next;

&

阅读以下函数说明和Java代码，将应填入(n)处的字句写在对应栏内。

  【说明】

 以下程序实现数据的排序，将n个整数分别按照升序和降序进行排序，类SortInt_1实现升序排序，类SortInt_2实现降序排序。

 【Java代码】

 class SortInt_1{

    int i,i,k,temp;

    void SortInt(int a1,int a2[]){//升序排序

       for(i=0;i＜a1-1;i++){

          k=i;

          for(j=i+1;j＜a1;j++){

            if((1)) k=j;

            if(k !=i){

               temp=a2[i];a2[i]=a2[k];a2[k]=temp;

            }

          }

       }

    }

 }

 class SortInt_2 (2) {

   int i,j,k,temp;

   void SortInt(int a1, int a2[]){//降序排序

     for(i=0; i＜a1-1;i++){

       k=i;

       for(j=i+1;j＜a1;j++){

          if((3))k=j;

       }

       if(k !=i){

          temp=a2[i];a2[i]=a2[k];a2[k]=temp;

       }

     }

   }

 }

 public class test{

   public static void main(String args[]){

     int a[]={10,55,100,35,87,90,100,16};

     SortInt_1 NewInt=(4);

     NewInt.SortInt(a.lenvh,a);//调用SortInt_1类的方法

     System.out.println("升序排列的数据: ");

     for(int i=0;i＜a.length;i++){

        System.out.print(a[i]+" ");

     }

     System.out.println();

     NewInt=new SortInt_2();//创建类SortInt_2的对象

     (5);//调用相应方法进行降序排序

     System.out.println("降序排列的数据: ");

     for(int i=0;i＜a.length;i++){

        System.out.print(a[i]+" ");

     }

   }

 }

阅读下列C程序和程序说明，将应填入(n)处的字句写在对应栏内。

 【说明】 应用Prim算法求解连通网络的最小生成树问题。请阅读程序后填空。

 const int MaxInt＝INT MAX；  //INT MAX的值在＜limits．h＞中

 const int n＝6；  //图的顶点数，应由用户定义

 typedef int AdjMatrix[n][n]；  //用二维数组作为邻接矩阵表示

 typedef struct{  //生成树的边结点

   int fromVex，to Vex；  //边的起点与终点

   int weight；  //边上的权值

 }TreeEdSenode；

 typedef TreeEdgeNode MST[n-1]；  //最小生成树定义

 void PrimMST (AdjMatrix G，MST T，int rt){

 //从顶点rt出发构造图G的最小生成树T，rt成为树的根结点

   TreeEdgeNode e； int i，k＝0，min，minpos，v；

   for(i＝0；i＜n；i++)  //初始化最小生成树T

    if(i!＝rt){

     T[k]．fromVex＝rt；

      (1)；

     T[k++].weight＝G[rt][i]；

    }

   for(k＝0；k＜n-1；k++){  //依次求MST的候选边

     (2)；

    for(i＝k；i＜n-1；i++)  八遍历当前候选边集合

     if(T[i].weight＜min)  //选具有最小权值的候选边

     {min＝T[i]．weight；(3)；}

    if(min＝＝MaxInt)  //图不连通，出错处理

     {cerr＜＜“Graph is disconnected!”＜＜endl； exit(1)；}

    e=T[minpos]；T[minpos]＝T[k]；(4)；

    v=T[k].to Vex；

    for(i＝k+1；i＜n-1；i++)  //修改候选边集合

     if(G[v][T[i].to Vex]＜T[i].weight){

      T[i]．weight＝G[v][T[i].toVex]；

       (5)；

     }

    }

 }

UML规定类图中类之间的关系有关联、聚集、继承，请说明它们的含义和之间的区别。

阅读以下说明，回答问题1和问题2，将解答写在对应栏内。

 【说明】

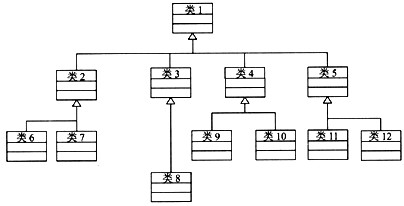
 一个野生动物园，有如下动物：老虎、豹、狼、丹顶鹤、鹦鹉、天鹅、金鱼、热带鱼、鳄鱼等等。

依据说明，完成下面的类图，要求第1层和第2层填写标识、主要属性和操作，第3层填写标识即可。

将该E-R图转换为关系模型。

阅读以下说明，回答问题1至问题3，将解答写在对应栏内。

 【说明】

 下面是某医院信息管理系统中需要的信息。

 科室：科名、科地址、科电话、医生姓名。

 病房：病房号、床位号、所属科室名。

 医生：姓名、职称、所属科室名、年龄、工作证号。

 病人：病历号、姓名、性别、诊断、主管医生、病房。

 其中，一个科室有多个病房，多个医生，一个病房只能属于一个科室，一个医生只属于一个科室，但可以负责多个病人的诊治，一个病人的主管医生只有一个。

画出上述信息涉及的E—R图。

指出每个关系模式的候选码。

指出在哪些图中遗漏了哪些数据流。回答时请用如下形式之一：

 XX图中遗漏了XX加工(或文件)流向XX加工(或文件)的XX数据流。

 XX加工XX遗漏了输入(或输出)数据流XX。

指出哪张图中的哪些文件不必画出。