●试题二

阅读下列说明、流程图和算法，将应填入(n)处的字句写在答题纸的对应栏内。

【说明】

下面的流程图(如图3所示)用N-S盒图形式描述了数组A中的元素被划分的过程。其划分方法是：以数组中的第一个元素作为基准数，将小于基准数的元素向低下标端移动，而大于基准数的元素向高下标端移动。当划分结束时，基准数定位于A[i]，并且数组中下标小于i的元素的值均小于基准数，下标大于i的元素的值均大于基准数。设数组A的下界为low，上界为high，数组中的元素互不相同。例如，对数组(4，2，8，3，6)，以4为基准数的划分过程如下：

【流程图】

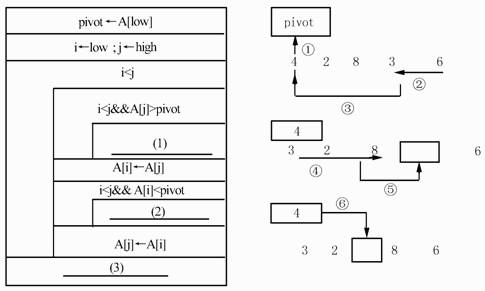
图3流程图

【算法说明】

将上述划分的思想进一步用于被划分出的数组的两部分，就可以对整个数组实现递增排序。设函数int p(int A[]，int low，int high)实现了上述流程图的划分过程并返回基准数在数组A中的下标。递归函数void sort(int A[]，int L，int H)的功能是实现数组A中元素的递增排序。

【算法】

void sort (int A[]， int 1，int H){

if ( L

k=p(A，L，R)；//p()返回基准数在数组A中的下标

sort( (4) )；//小于基准数的元素排序

sort( (5) )；//大于基准数的元素排序

}

}

●试题五

阅读下列程序说明和C代码，将应填入(n)处的字句写在答卷的对应栏内。

【程序5说明】

下列文法可用来描述化学分子式的书写规则(例如，Al2(CO₃)₃、Cu(OH)₂)：

λ→β\βλβ→δ\δn

δ→ξ\ξθ＼(λ)

其中：λ是一个分子式；δ或是一个元素，或是一个带括号的(子)分子式，元素或是一个大写字母(记为ξ)，或是一个大写字母和一个小写字母(记为ξθ)；β或是一个δ，或是在δ之后接上一个整数n，δn表示β有n个δ的元素或(子)分子式。一个完整的分子式由若干个β组成。

当然一个正确的分子式除符合上述文法规则外，还应满足分子式本身的语义要求。

下面的程序输入分子式，按上述文法分析分子式，并计算出该分子式的分子量。例如：元素H的原子量是1，元素O的原子量是16。输入分子式H₂O，程序计算出它的分子量为18(1×2+16)。程序中各元素的名及它的原子量从文件atom.dat中读入。

【程序5】

#include

#include

#define MAXN 300

#define GMLEN 30

struct elem{char name［］;/*元素名*/

doublev；/*原子量*/

}nTbl［MAXN］；

char cmStr［GMLEN］，*pos;

int c;FILE*fp;

double factor();

double atom()/*处理文法符号δ*/

{char w［3］;int i;double num;

while((c=*pos++)==′||c==′＼t′);/*略过空白字符*/

if(c==′＼n′)return 0.0;

if(c>=′A′ && C<=′Z′){/*将元素名存入W*/

w［i=0］=c;c=*pos++;

if(c>=′a ′&& c<=′z′)w［++i］=c;else pos--;

w［++i］=′＼0′;

for(i=0；nTbl［i］.v>0.0;i++)

if(strcmp(w，nTb［i］.name)==0)returnnTbl［i］.v；

printf("＼n元素表中没有所输入的元素：＼t%s＼n",w);retur n-1.0;

}elseif(c==′(′){

if((num= (1) )<0.0)return-1.0;/*包括可能为空的情况*/

if(*pos++!=′)′){printf("分子式中括号不匹配！/n")；return-1.0；}

returnnum;

}

printf("分子式中存在非法字符：＼t%c＼n",c)；

return-1.0;

}

double mAtom()/*处理文法符号β*/

{double num;int n=1;

if((num= (2) )<0.0)return-1.0;

c=*pos++；

if(c>=′0′&&c<=′9′){

n=0;while(c>=0&&c<=′9′)

{n= (3) ；

c=*poss++;

}

}

pos--;

return num*n;

}

double factor()/*处理文法符号λ*/

{double num=0.0,d;

if((num=mAtom())<0.0)return-1.0;

while(*pos>=′A′&&*pos<=′Z′||*pos==′(′){

if((d= (4) )<0.0)return-1.0；

 (5) ；

}return num；

}

void main()

{char fname［］="atom.dat";/*元素名及其原子量文件*/

int i;double num；

if((fp=fopen(fname,"r"))==NULL){/*以读方式打开正文文件*/

printf("Can not open%s file.＼n",fname);return/*程序非正常结束*/

}

i=0；

while(i

i++;

fclose(fp);nTbl［i］.v=-1.0;

while (1) {/*输入分子式和计算分子量循环，直至输入空行结束*/

printf("＼n输入分子式！(空行结束)＼n");gets(cmStr);

pos=cmStr;

if(cmStr［0］==′＼0′)break；

if((num=fator())>0.0)

if(*pos!=′＼0′)printf("分子式不完整！＼n")；

 else printf("分子式的分子量为%f＼n",num)；

}

}

●试题四

阅读下列算法说明和算法，将应填入(n)的字句写在答题纸的对应栏内。

【说明】

下列最短路径算法的具体流程如下：首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择不使森林中产生回路的边加入到森林中去，直至该森林变成一棵树为止，这棵树便是连通网的最小生成树。该算法的基本思想是：为使生成树上总的权值之和达到最小，则应使每一条边上的权值尽可能地小，自然应从权值最小的边选起，直至选出n-1条互不构成回路的权值最小边为止。

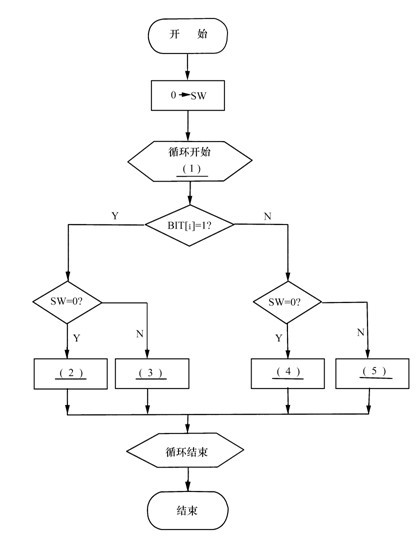
图5算法流程图

【算法】

/*对图定义一种新的表示方法，以一维数组存放图中所有边，并在构建图的存储结构时将它构造为一个"有序表"。以顺序表MSTree返回生成树上各条边。*/

typedef struct{

VertexType vex1；

VertexType vex2；

VRType weight；

}EdgeType；

typedef ElemType EdgeType；

typedef struct{//有向网的定义

VertexType vexs[MAX_VERTEX_NUM]；//顶点信息

EdgeType edge[MAX_EDGE_NUM]；//边的信息

int vexnum，arcnum；//图中顶点的数目和边的数目

}ELGraph；

void MiniSpanTree_Kruskal(ELGraph G，SqList& MSTree){

//G.edge 中依权值从小到大存放有向网中各边

//生成树的边存放在顺序表MSTree中

MFSetF；

InitSet(F，G.vexnum)；//将森林F初始化为n棵树的集合

InitList(MSTree，G.vexnum)；//初始化生成树为空树

i=0；k=1；

while(k< (1) ){

e=G.edge[i]；//取第i条权值最小的边

/*函数fix_mfset返回边的顶点所在树的树根代号，如果边的两个顶点所在树的树根相同，则说明它们已落在同一棵树上。*/

rl=fix_mfset(F，LocateVex(e.vex1))；

r2= (2) //返回两个顶点所在树的树根

if(r1 (3) r2){//选定生成树上第k条边

if(ListInsert(MSTree，k，e){ (4) ；//插入生成树

mix_mfset(E，rl，r2)；//将两棵树归并为一棵树

}

     (5) ；//继续考察下一条权值最小边

   }

DestroySet(F)；

}

●试题三

阅读下列说明，回答问题1至问题4，将解答填入答题纸的对应栏内。

【说明】

甲公司的经营销售业务目前是手工处理的，随着业务量的增长，准备采用关系数据库对销售信息进行管理。经销业务的手工处理主要涉及三种表：订单、客户表和产品表(见表2，表3和表4)。

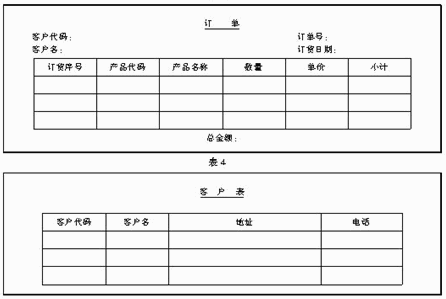
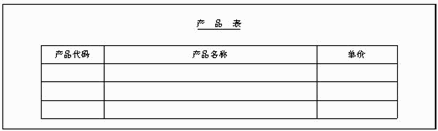
为了用计算机管理销售信息，甲公司提出应达到以下要求：产品的单价发生变化时，应及时修改产品表中的单价数据。客户购货计价采用订货时的单价。订货后，即使单价发生变化，计算用的单价也不变。

在设计数据库时，经销部的王先生建立了如图4所示的数据模型。其中，方框表示实体，单向箭头表示1对多的联系，双向箭头表示多对多的联系。

由于上述模型对建立关系数据库是不合适的，因此王先生又修改了数据模型，并设计了如下几个关系(带下划线的数据项是关键项，最后一个关系中没有指出关键项)：

Customer(CustomerNo,CustomerName,Address,Phone)

Product(ProductNo,ProductName,UnitPrice)

Order(OrderNo,CustomerNo,Date)

OrderDetail(OrderNo,ProductNo,Quantity)

【问题1】

请按【说明】中的要求画出修改后的数据模型。

【问题2】

 (1) 【说明】中的几个关系仍无法实现甲公司的要求，为什么？

 (2) 需要在哪个关系中增加什么数据项才能实现这个要求？

【问题3】

写出OrderDetail中的关键项。

【问题4】

以下SQL语句用于查询没有订购产品代码为"1K10"的产品的所有客户名。请填补其中的空缺。

SELECT CustomerName FROM Customer (1) 

WHERE (2) 

(SELECT*FROM OrderDetail B,Order C

WHERE

   B．ProductNo=

   C．ProductNo

AND

   B．ProductNo=′1K10′

AND

   C．CustomerNo=A．CustomerNo)

●试题一

阅读下列说明和有关的图表，回答问题1至问题3，将解答填入答题纸的对应栏内。

【说明】

A公司决定为该市车站开发自动售票系统，系统的要求如下：

1.乘客能按以下三步操作购票：选定目的地；投入钱币；获得一张票；

2.当且仅当乘客选定目的地后，系统才接收投钱，每次投入的钱只购买一张票；

3.只要投入的钱不少于所需的票价，且票库中有所要求的票，则应尽快出票；

4.如需找钱，则在出票的同时应退还多余的钱；

5.如果乘客投入的钱不够票价，或者票库中没有所要求的票时，系统将全额退钱，并允许乘客另选目的地，继续购票；

6.出票前乘客可以按"取消"按钮取消购票，系统将全额退出该乘客投入的钱，并允许乘客另选目的地，继续购票；

7.出票结束(包括退还多余的钱)后，系统应保存销售记录，并等待乘客购票。

该系统还要求快速响应和操作同步，所以它应是一个实时系统。为此，A公司在该系统的数据流程图中附加了过程控制部分，形成转换图。在该图中，控制流(事件流)用虚线表示，数据流用实线表示。图中的数据流并没有画全，需要考生填补。转换图如图1所示。

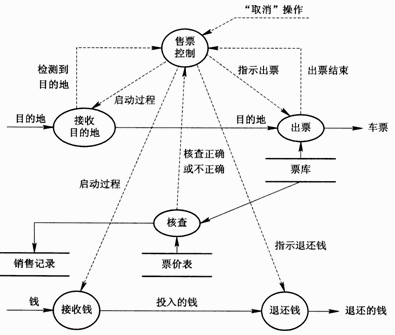
图1转换图

程进行的控制可以用系统内部各个状态之间的迁移来描述，从而形成状态迁移图。在状态迁移图中，用双线框表示状态，用有向边表示状态的迁移。引起状态迁移的事件以及由该事件引起的动作，在有向边旁用"事件  动作"形式注明。状态迁移图如图2所示。

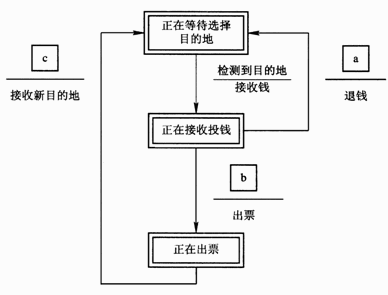
图2状态迁移图

该公司还制作了一个过程启动表，用以表明状态迁移图中的4个动作与转换图中的4个过程之间的"启动"关系，即说明哪个动作将启动哪个过程。用1表示启动，用0表示不启动。启动的过程将根据获得的输入数据产生输出数据，未启动的过程则不会产生输出数据。该表中没有列出的过程，其执行与否与事件无关。过程启动表见表1：

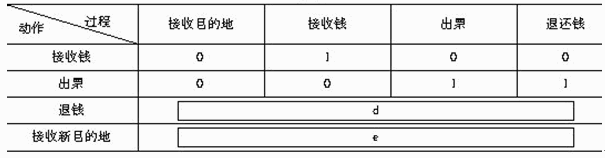
【问题1】

转换图中缺少哪三条数据流?请指明每条数据流的名称、起点和终点。

【问题2】

在状态迁移图中，a，b，c分别表示什么事件？请用转换图中给出的事件名解答。

【问题3】

在过程启动表中，d，e处应填什么?请分别用4位二进制码表示。

●试题二

阅读下列说明、流程图和算法，将应填入(n)处的字句写在答题纸的对应栏内。

【说明】

下面的流程图(如图3所示)用N-S盒图形式描述了数组A中的元素被划分的过程。其划分方法是：以数组中的第一个元素作为基准数，将小于基准数的元素向低下标端移动，而大于基准数的元素向高下标端移动。当划分结束时，基准数定位于A[i]，并且数组中下标小于i的元素的值均小于基准数，下标大于i的元素的值均大于基准数。设数组A的下界为low，上界为high，数组中的元素互不相同。例如，对数组(4，2，8，3，6)，以4为基准数的划分过程如下：

【流程图】

图3流程图

【算法说明】

将上述划分的思想进一步用于被划分出的数组的两部分，就可以对整个数组实现递增排序。设函数int p(int A[]，int low，int high)实现了上述流程图的划分过程并返回基准数在数组A中的下标。递归函数void sort(int A[]，int L，int H)的功能是实现数组A中元素的递增排序。

【算法】

void sort (int A[]， int 1，int H){

if ( L

k=p(A，L，R)；//p()返回基准数在数组A中的下标

sort( (4) )；//小于基准数的元素排序

sort( (5) )；//大于基准数的元素排序

}

}