设A,B,C为三个随机事件,P(A)=P(B)=P(C)=1/4,P(AB)=P(AC)=P(BC)=1/6,P(ABC)=0,则P(A∪B∪C)=________。
-
某大学从来自A,B两市的新生中分别随机抽取5名与6名新生,测其身高(单位:cm)后算得
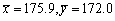 ;s12=11.3,s22=9.1。假设两市新生身高分别服从正态分布X~N(μ1,σ2),Y~N(μ2,σ2),其中σ2未知。
;s12=11.3,s22=9.1。假设两市新生身高分别服从正态分布X~N(μ1,σ2),Y~N(μ2,σ2),其中σ2未知。试求μ1-μ2的置信度为0.95的置信区间。(t0.025(9)=2.2622,t0.025(11)=2.2010)
-
设随机变量X的概率密度为,
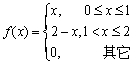 ,
,求:(1)X的分布函数F(x);
(2)P{X<0.5},p{x>1.3}。
-
设二维随机向量(X,Y)的联合分布列为
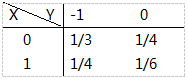
试求:(1)(X,Y)关于X和关于Y的边缘分布列;
(2)X与Y是否相互独立?为什么?
(3)P{X+Y=0}。
-
设随机变量X的概率密度为
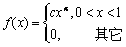 ,且E(X)=0.75,求常数c和α。
,且E(X)=0.75,求常数c和α。 -
设某地区地区男性居民中肥胖者占25%,中等者占60%,瘦者占15%,又知肥胖者患高血压病的概率为20%,中等者患高血压病的概率为8%,瘦者患高血压病的概率为2%,试求:
(1)该地区成年男性居民患高血压病的概率;
(2)若知某成年男性居民患高血压病,则他属于肥胖者的概率有多大?
-
设总体X服从正态分布N(0,0.25),X1,X2,…,X7为来自该总体的一个样本,要使
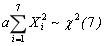 ,则应取常数a=________。
,则应取常数a=________。 -
设二维随机向量(X,Y)的概率密度为
 ;则当0≤y≤1时,(X,Y)关于Y的边缘概率密度fY(y)=________。
;则当0≤y≤1时,(X,Y)关于Y的边缘概率密度fY(y)=________。 -
设总体X的分布列为
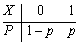 ,其中p为未知参数,且
,其中p为未知参数,且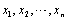 为其样本,则p的矩
为其样本,则p的矩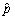 估计=________。
估计=________。 -
设总体X~N(μ,σ2),
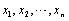 为来自总的样本,
为来自总的样本,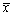 为样本均值,则D(
为样本均值,则D(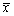 )=________。
)=________。 -
已知二维随机向量(X,Y)服从区域G:0≤x≤1,0≤y≤2上的均匀分布,则
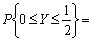 ________。
________。
2005年初级经济师考试《旅游经济专
初级旅游经济师试题及答案一
初级旅游经济师试题及答案二
2005年初级经济师考试《邮电经济专
初级经济师试题及答案1(邮电经济)
初级经济师试题及答案1(保险经济)
初级经济师试题及答案2(邮电经济)
初级经济师试题及答案2(保险经济)
初级经济师试题及答案3(保险经济)
2014年经济师初级考试真题《建筑经
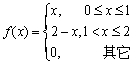 ,
,