设二维随机变量(X,Y)的概率密度为![]() ,则常数c=________。
,则常数c=________。
-
某厂生产的一种金属丝,其折断力X(单位:kg)服从正态分布N(μ,σ2),以往的平均折断力μ=570,今更换原材料生产一批金属丝,并从中抽出9个样品检测折断力,算得样本均值
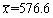 ,样本标准差s=7.2。试问更换原材料后,金属丝的平均折断力是否有显著变化?(附:α=0.05,
,样本标准差s=7.2。试问更换原材料后,金属丝的平均折断力是否有显著变化?(附:α=0.05,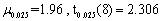 )
) -
设随机变量X~N(1,9),Y~N(0,16),且X与Y的相关系数为
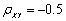 ,
,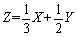 。
。 求:
(1)Cov(X,Y);
(2)E(Z),D(Z);
(3)Cov(X,Z)。
-
设随机变量X的概率密度为,且E(X)=1/2。
求:
(1)常数a,b;
(2)D(X)
-
设二维随机变量(X,Y)的分布律为
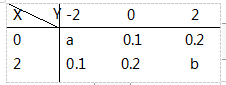
P{X=2}=0.6。
求:
(1)常数a,b;
(2)(X,Y)关于Y的边缘分布律;
(3)P{X+Y≤0}。
-
两台车床加工同一种零件,第一台出现次品的概率是0.03,第二台出现次品的概率是0.06,加工出来的零件混放在一起,第一台加工的零件数是第二台加工的零件数的两倍。
求:
( 1 ) 从中任取一个零件是次品的概率;
( 2 ) 若取得的零件是次品,它是由第一台加工的概率。
-
设
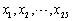 为来自正态总体N(μ,52)的样本,
为来自正态总体N(μ,52)的样本, 为样本均值,欲检验假设
为样本均值,欲检验假设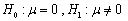 ,则应采用的检验统计量的表达式为________。
,则应采用的检验统计量的表达式为________。 -
设
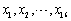 为来自正态总体N(0,1)的样本,则
为来自正态总体N(0,1)的样本,则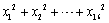 服从的分布是________。
服从的分布是________。 -
设
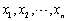 为来自总体X的样本,
为来自总体X的样本,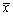 是样本均值,若X服从[0,4θ]上的均匀分布,θ>0,则未知参数θ的矩估计
是样本均值,若X服从[0,4θ]上的均匀分布,θ>0,则未知参数θ的矩估计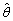 =________。
=________。 -
设总体X服从参数是λ的指数分布,
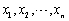 为来自X的样本,
为来自X的样本,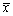 是样本均值,则
是样本均值,则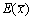 =________。
=________。 -
设X~B(100,0.2),Y=(X-20)/4,由中心极限定理知Y近似服从的分布是________。
2005年初级经济师考试《旅游经济专
初级旅游经济师试题及答案一
初级旅游经济师试题及答案二
2005年初级经济师考试《邮电经济专
初级经济师试题及答案1(邮电经济)
初级经济师试题及答案1(保险经济)
初级经济师试题及答案2(邮电经济)
初级经济师试题及答案2(保险经济)
初级经济师试题及答案3(保险经济)
2014年经济师初级考试真题《建筑经

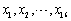 为来自正态总体N(0,1)的样本,则
为来自正态总体N(0,1)的样本,则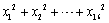 服从的分布是________。
服从的分布是________。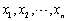 为来自总体X的样本,
为来自总体X的样本,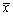 是样本均值,若X服从[0,4θ]上的均匀分布,θ>0,则未知参数θ的矩估计
是样本均值,若X服从[0,4θ]上的均匀分布,θ>0,则未知参数θ的矩估计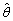 =________。
=________。