线性代数(经管类)2018年10月真题试题及答案解析(04184)
部分试题预览
相关试卷
2019年4月外刊经贸知识选读真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2008年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2009年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2009年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2010年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2010年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2011年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2011年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2012年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2012年7月真题试
所属类型:真题考试2021-03-24
 可逆,证明线性方程组
可逆,证明线性方程组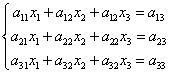 无解.
无解.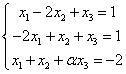 有无穷多解?并求出其通解.(要求用它的一个特解和导出组的基础解系表示)
有无穷多解?并求出其通解.(要求用它的一个特解和导出组的基础解系表示)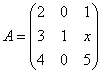 可相似对角化,求数x.
可相似对角化,求数x.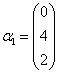 ,
,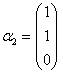 ,
,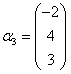 ,
,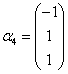 的一个极大线性无关组,并将其余向量由该极大线性无关组线性表出.
的一个极大线性无关组,并将其余向量由该极大线性无关组线性表出.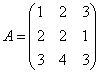 ,
,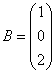 ,求X.
,求X.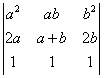 的值.
的值.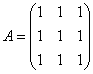 的非零特征值λ=________.
的非零特征值λ=________.