工程力学(二)2007年4月真题(02391)
-
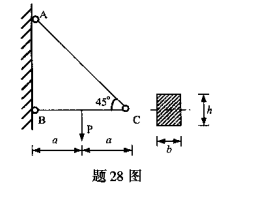
图示结构中,BC为矩形截面杆,已知a=1m,b=120mm,h=160mm,材料的容许应力[σ]=10MPa,P=8kN,试校核BC杆的强度。
-
圆形截面轴向受压杆如图所示,其下端固定,上端铰支(球铰),已知ι=1m,d=22mm,
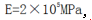 ,λp=100,稳定安全系数K=3,试根据稳定条件确定压杆容许荷载[P]。
,λp=100,稳定安全系数K=3,试根据稳定条件确定压杆容许荷载[P]。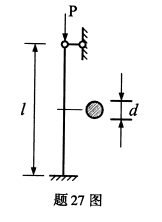
-
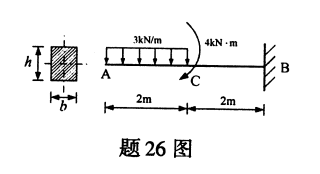
矩形截面梁AB受力如图所示,其中力偶作用在AB中点C截面处。已知梁的宽度b=140mm,高度h=280mm,材料的容许应力[σ]=10MPa。
(1)作梁的剪力图和弯矩图;
(2)校核该梁的正应力强度。
-
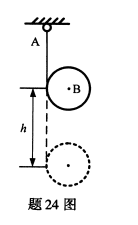
均质圆盘B质量为m,半径为R,其上绕有细绳(不计绳重)悬挂在固定点A处,若使圆盘从图示实线位置无初速下落高度h至图示虚线位置,试用动能定理求该瞬时轮心的下降速度。
-
图示桁架,受铅垂载荷P=50kN作用,杆1,2的横截面均为圆形,其直径分别为d1=15mm、d2=20mm,材料的容许应力均为[σ]=150MPa.试校核桁架的强度。

-
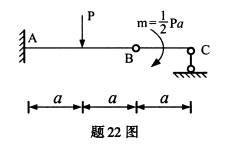
结构的尺寸及荷载如图所示,试求链杆支座C和固定端A的约束反力。
-
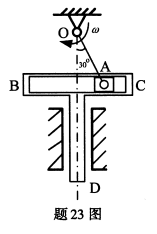
曲柄滑道机构中,OA=r的曲柄以角速度ω绕O点转动,通过滑块A带动滑槽BCD往复运动,试求图示瞬时滑槽BCD的速度。
-
受力杆件中围绕某点截取的单元体如图所示,该点的最大主应力σ′主=( )。
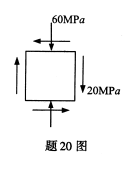
-
直径为d的实心杆受力如图所示,已知m1和m2,根据第三强度理论,外表面上C点的相当应力σxd3=( )。
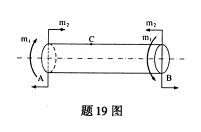
-
梁ABCD尺寸及荷载如图所示,试求支座A、B处的约束反力。
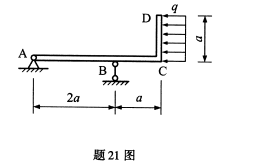
-
若AB梁在B支座处的下沉量为δ,则B处的约束力为( )。

-
在研究构件的强度、刚度和稳定性时,对变形体作了连续性假设、均匀性假设和( )。
-
图示A和B的直径都为d,则两者中的较大剪应力的大小等于( )。
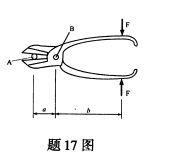
-
如果在质点系的虚位移上,约束反力的虚功之和等于零,则把这种约束称为( )。
-
质量为m的均质薄板尺寸如图所示,已知它对沿其边界的y’轴的转动惯量
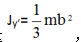 ,则它对过其形心且平行于y’轴的y轴的转动惯量应为( )。
,则它对过其形心且平行于y’轴的y轴的转动惯量应为( )。
-
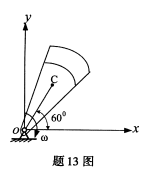
图示偏心轮质量为m,绕轴O转动的角速度为ω,质心C与轴O连线OC=e,当OC与x轴成60°角时,其动量在x轴上的投影px=( )。
-
用基点法求平面图形上某点的加速度时,任一点的加速度等于基点的加速度与该点绕基点作圆周运动的加速度的矢量和,后者一般由两部分组成,这两部分分别是绕基点作圆周运动的( )。
-
等截面直梁在弯曲变形时,挠曲线的最大曲率发生在()
- A.挠度最大的横截面
- B.转角最大的横截面
- C.剪力最大的横截面
- D.弯矩最大的横截面
-
构件作匀加速直线运动时,其动应力和相应的静应力之比,即动荷系数Kd的大小为()
- A.Kd=0
- B.0<Kd<1
- C.Kd=1
- D.Kd>1
-
力偶对其作用面内任意一点之矩都等于该力偶的( )。
-
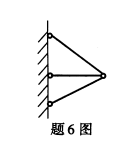
图示结构为()
- A.静定结构
- B.一次超静定结构
- C.二次超静定结构
- D.三次超静定结构
-
轴向拉伸杆,正应力最大的截面和剪应力最大的截面()
- A.分别是横截面、45°斜截面
- B.都是横截面
- C.分别是45°斜截面、横截面
- D.都是45°斜截面
-
在下列关于平面图形几何性质的结论中,错误的是()
- A.图形的对称轴必通过形心
- B.图形两个对称轴的交点必为形心
- C.图形对对称轴的静矩为零
- D.使静矩为零的轴一定是对称轴
-
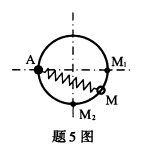
弹簧刚度系数为k,一端固定在半径为R的圆环的A点,另一端连接小环M,小环M套在圆环上,已知弹簧原长I0=R,则小环M从图中的M1点运动到M2点时,弹性力的功等于()
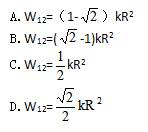
- A.A
- B.B
- C.C
- D.D
-
平面连杆机构中
 ,若O1A以匀角速度w绕O1转动,则连杆AB中点C的速度和加速度的大小分别为()
,若O1A以匀角速度w绕O1转动,则连杆AB中点C的速度和加速度的大小分别为()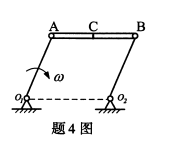

- A.A
- B.B
- C.C
- D.D
-
动点的运动方程为:
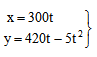 (单位:m),则t=2秒时其速度v的大小应等于()
(单位:m),则t=2秒时其速度v的大小应等于()- A.500m/s
- B.420m/s
- C.400m/s
- D.300m/s
-
物体A重量为Q,置于水平面上,接触面上的静滑动摩擦系数f=0.32,在物体上施加一水平拉力P=0.3Q,则接触面上的摩擦力F为()
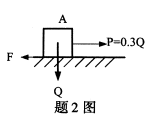
- A.F=0
- B.F=0.3Q
- C.F=0.32Q
- D.F=Q
-
平面汇交力系如图所示,已知F1=
 ,F2=1kN,F3=3kN,则该力系的合力R的大小应为()
,F2=1kN,F3=3kN,则该力系的合力R的大小应为()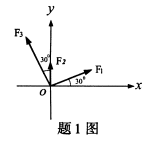
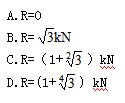
- A.A
- B.B
- C.C
- D.D
















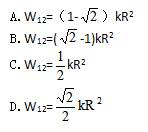


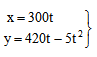 (单位:m),则t=2秒时其速度v的大小应等于()
(单位:m),则t=2秒时其速度v的大小应等于()