线性代数(经管类)2010年4月真题试题及答案解析(04184)
-
设A,B,A+B均为n阶正交矩阵,证明
 .
. -
设矩阵
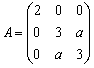 的三个特征值分别为1,2,5,求正的常数a的值及可逆矩阵P,使
的三个特征值分别为1,2,5,求正的常数a的值及可逆矩阵P,使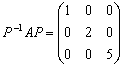 .
. -
已知矩阵
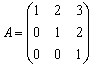 ,
, .(1)求
.(1)求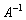 ;(2)解矩阵方程AX=B.
;(2)解矩阵方程AX=B. -
问a为何值时,线性方程组
 有惟一解?有无穷多解?并在有解时求出其解(在有无穷多解时,要求用一个特解和导出组的基础解系表示全部解).
有惟一解?有无穷多解?并在有解时求出其解(在有无穷多解时,要求用一个特解和导出组的基础解系表示全部解). -
计算行列式
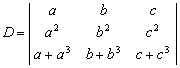 的值.
的值. -
已知矩阵B=(2,1,3),C=(1,2,3),求(1)A=BTC;(2)A2.
-
设向量组
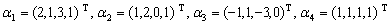 ,求向量组的秩及一个极大线性无关组,并用该极大线性无关组表示向量组中的其余向量.
,求向量组的秩及一个极大线性无关组,并用该极大线性无关组表示向量组中的其余向量. -
二次型
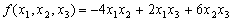 的矩阵是
的矩阵是 -
已知
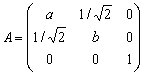 是正交矩阵,则a+b=___________.
是正交矩阵,则a+b=___________. -
设矩阵
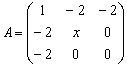 的特征值为4,1,-2,则数x=______.
的特征值为4,1,-2,则数x=______. -
齐次线性方程组
 的基础解系所含解向量的个数为___________.
的基础解系所含解向量的个数为___________. -
设n阶可逆矩阵A的一个特征值是-3,则矩阵
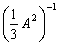 必有一个特征值为 .
必有一个特征值为 . -
设A为n阶矩阵,B为n阶非零矩阵,若B的每一个列向量都是齐次线性方程组Ax=0的解,则|A|=._________.
-
设A为n阶可逆矩阵,且
 ,则|A-1|= .
,则|A-1|= . -
设矩阵
 ,
, ,则ATB=
,则ATB= -
行列式
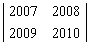 的值为_____________.
的值为_____________. -
设
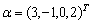 ,
, ,若向量γ满足
,若向量γ满足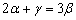 ,则γ= .
,则γ= . -
设A为可逆矩阵,则与A必有相同特征值的矩阵为( )
- A.AT
- B.A2
- C.A-1
- D.A*
-
二次型
 的正惯性指数为( )
的正惯性指数为( )- A.0
- B.1
- C.2
- D.3
-
下列命题中错误的是( )
- A.只含有1个零向量的向量组线性相关
- B.由3个2维向量组成的向量组线性相关
- C.由1个非零向量组成的向量组线性相关
- D.2个成比例的向量组成的向量组线性相关
-
已知向量组α1,α2,α3线性无关,α1,α2,α3,β线性相关,则( )
- A.α1必能由α2,α3,β线性表出
- B.α2必能由α1,α3,β线性表出
- C.α3必能由α1,α2,β线性表出
- D.β必能由α1,α2,α3线性表出
-
设A为m*n矩阵,m≠n,则方程组Ax=0只有零解的充分必要条件是A的秩( )
- A.小于m
- B.等于m
- C.小于n
- D.等于n
-
 ,
, ,
, ,
, ,则B=( )
,则B=( )- A.PA
- B.AP
- C.QA
- D.AQ
-
已知A是一个3*4矩阵,下列命题中正确的是( )
- A.若矩阵A中所有3阶子式都为0,则秩(A)=2
- B.若A中存在2阶子式不为0,则秩(A)=2
- C.若秩(A)=2,则A中所有3阶子式都为0
- D.若秩(A)=2,则A中所有2阶子式都不为0
-
设A , B , C均为n阶方阵,AB=BA,AC=CA,则ABC=( )
- A.ACB
- B.CAB
- C.CBA
- D.BCA
-
设A为3阶方阵,B为4阶方阵,且|A|=1,|B|=-2,则行列式|B||A|之值为( )
- A.-8
- B.-2
- C.2
- D.8
-
已知2阶行列式
 ,
,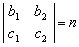 ,则
,则 ( )
( )- A.m-n
- B.n-m
- C.m+n
- D.-(m+n)
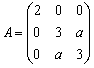 的三个特征值分别为1,2,5,求正的常数a的值及可逆矩阵P,使
的三个特征值分别为1,2,5,求正的常数a的值及可逆矩阵P,使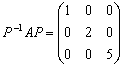 .
.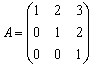 ,
, .(1)求
.(1)求 有惟一解?有无穷多解?并在有解时求出其解(在有无穷多解时,要求用一个特解和导出组的基础解系表示全部解).
有惟一解?有无穷多解?并在有解时求出其解(在有无穷多解时,要求用一个特解和导出组的基础解系表示全部解).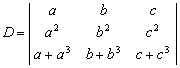 的值.
的值.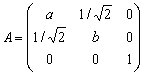 是正交矩阵,则a+b=___________.
是正交矩阵,则a+b=___________.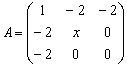 的特征值为4,1,-2,则数x=______.
的特征值为4,1,-2,则数x=______. ,
, ,
, ,
, ,则B=( )
,则B=( )