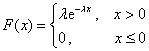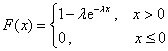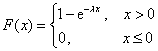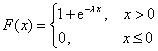概率论与数理统计(经管类)2012年4月真题
-
某生产线上的产品按质量情况分为A,B,C三类.检验员定时从该生产线上任取2件产品进行抽检,若发现其中两件全是A类产品或一件A类一件B类产品,就不需要调试设备,否则需要调试。
已知该生产线上生产的每件产品为A类品、B类品和C类品的概率分别为0.9,0.05和0.05,且各件产品的质量情况互不影响。
求:(1) 抽到的两件产品都为B类品的概率P?;
(2) 抽检后设备不需要调试的概率P?。
-
设总体X的概率密度
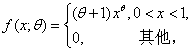 其中未知参数θ>-1,
其中未知参数θ>-1,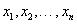 是来自该总体的一个样本,求参数θ的矩估计和极大似然估计。
是来自该总体的一个样本,求参数θ的矩估计和极大似然估计。 -
随机变量X与Y相互独立,且都服从标准正态分布,令
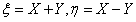
求:(1)
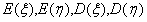 ;(2)
;(2)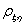
-
设二维随机变量(X,Y)的分布律为
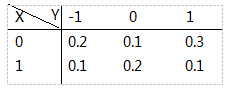
-
在假设检验中,犯第一类错误的概率为0.01,则在原假设H0成立的条件下,接受H0的概率为________。
-
随机变量X的概率密度为
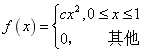
求:(1) 常数c;(2) X的分布函数F(x);(3)
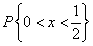
-
设总体X~N(0,1),x1、x2、x3为来自总体X的一个样本,且
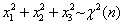 ,则n=________。
,则n=________。 -
设总体X~N(μ,1),x1、x2为来自总体X的一个样本,估计量
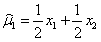 ,
,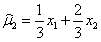 ,则方差较小的估计量是________。
,则方差较小的估计量是________。 -
设总体X服从二项分布B(2,0.3),
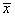 为样本均值,则
为样本均值,则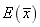 =________。
=________。 -
设随机变量X的分布律为
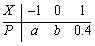 ,a、b为常数,且E(X)=0,则a-b=________。
,a、b为常数,且E(X)=0,则a-b=________。 -
设随机变量X~N(1,1),应用切比雪夫不等式估计概率
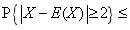 ________。
________。 -
设随机变量X服从参数为3的泊松分布,则E(X-3)=________。
-
设二维随机变量(X,Y)的分布律为

则P{X=Y}=________。
-
设二维随机变量(X,Y)的分布函数为
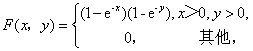 ,
,则P{X≤1,Y≤1}=________。
-
设随机变量X的分布律为
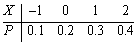 ,则P{x≥1)=________。
,则P{x≥1)=________。 -
设二维随机变量(X,Y)在区域D上服从均匀分布,其中D:0≤x≤2,0≤y≤2。记(X,Y)的概率密度为f(x,y),则f(1,1)=________。
-
设A,B为随机事件,P(A)=0.5,P(B)=0.4,P(A|B)=0.8,则P(B|A)=________。
-
设袋中有2个黑球、3个白球,有放回地连续取2次球,每次取一个,则至少取到一个黑球的概率是________。
-
设随机事件A与B相互独立,且
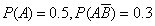 ,则P(B)=________。
,则P(B)=________。 -
设样本
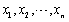 来自正态总体N(μ,σ2),且σ2未知,
来自正态总体N(μ,σ2),且σ2未知,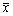 是样本均值,s2为样本方差,假设检验问题为
是样本均值,s2为样本方差,假设检验问题为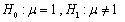 ,则采用的检验统计量为()
,则采用的检验统计量为()- A.
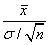
- B.
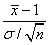
- C.
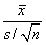
- D.
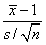
- A.
-
在一次读书活动中,某同学从2本科技书和4本文艺书中任选2本,则选中的书都是科技书的概率为________。
-
设总体X~N(2,32),为来自总
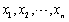 体X的样本,
体X的样本,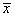 为样本均值,则下列统计量中服从标准正态分布的是()
为样本均值,则下列统计量中服从标准正态分布的是()- A.
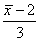
- B.
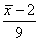
- C.
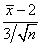
- D.
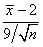
- A.
-
设随机变量X的方差D(X)存在,且D(X)>0,令Y=-X,则
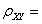 ()
()- A.-1
- B.0
- C.1
- D.2
-
设随机变量X与Y相互独立,它们的概率密度分别为
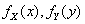 ,则(X,Y)的概率密度为()
,则(X,Y)的概率密度为()- A.
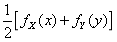
- B.
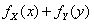
- C.
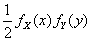
- D.

- A.
-
设随机变量X的分布函数为F(x),则()
- A.F(-∞)=1
- B.F(0)=0
- C.F(+∞)=0
- D.F(+∞)=1
-
设随机变量X~B(n,p),且E(X)=2.4,D(X)=1.44,则参数n,p的值分别为()
- A.4和0.6
- B.6和0.4
- C.8和0.3
- D.3和0.8
-
设随机变量X的概率密度为
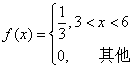 ,则P{3
,则P{3- A.P{1
- B.P{4
- C.P{3
- D.P{2
- B.P{4
- A.P{1
-
已知随机变量X服从参数为λ的指数分布,则X的分布函数为()
- A.
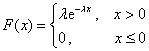
- B.
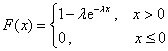
- C.
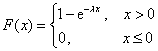
- D.
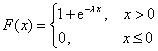
- A.
-
设A,B为B为随机事件,且
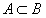 ,则
,则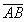 等于()
等于()- A.
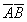
- B.
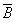
- C.

- D.A
- A.
-
设A,B为随机事件,则P(A-B)=()
- A.P(A)-P(B)
- B.P(A)-P(AB)
- C.P(A)-P(B)+P(AB)
- D.P(A)+P(B)-P(AB)
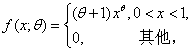 其中未知参数θ>-1,
其中未知参数θ>-1,
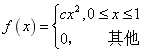

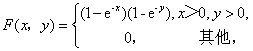 ,
,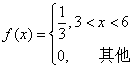 ,则P{3
,则P{3