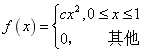设总体X的概率密度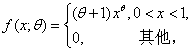 其中未知参数θ>-1，是来自该总体的一个样本，求参数θ的矩估计和极大似然估计。

某生产线上的产品按质量情况分为A，B，C三类．检验员定时从该生产线上任取2件产品进行抽检，若发现其中两件全是A类产品或一件A类一件B类产品，就不需要调试设备，否则需要调试。

已知该生产线上生产的每件产品为A类品、B类品和C类品的概率分别为0.9，0.05和0.05，且各件产品的质量情况互不影响。

求：(1) 抽到的两件产品都为B类品的概率P?；

(2) 抽检后设备不需要调试的概率P?。

设总体X的概率密度 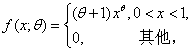其中未知参数θ>-1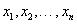，是来自该总体的一个样本，求参数θ的矩估计和极大似然估计。

随机变量X与Y相互独立，且都服从标准正态分布，令

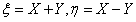
求：(1)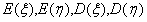;(2)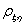

设二维随机变量(X，Y)的分布律为

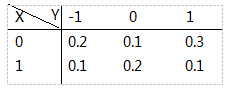
在假设检验中，犯第一类错误的概率为0.01，则在原假设H₀成立的条件下，接受H₀的概率为________。

随机变量X的概率密度为

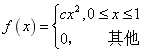
求：(1) 常数c；(2) X的分布函数F(x)；(3)

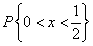
设总体X~N(0，1)，x₁、x₂、x₃为来自总体X的一个样本，且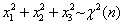，则n=________。

设总体X~N(μ，1)，x₁、x₂为来自总体X的一个样本，估计量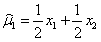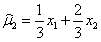，，则方差较小的估计量是________。

设总体X服从二项分布B(2，0.3)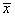，为样本均值，则=________。

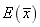设随机变量X的分布律为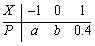，a、b为常数，且E(X)=0，则a-b=________。