主观
求线性方程组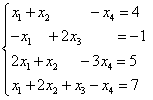 的通解。(要求用它的一个特解和导出组的基础解系表示)
的通解。(要求用它的一个特解和导出组的基础解系表示)
相关试题
-
用配方法化二次型
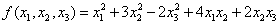 为标准形,并写出所作的可逆线性变换。
为标准形,并写出所作的可逆线性变换。 -
设2是矩阵A的特征值,若|A|=4,证明2也是矩阵A*的特征值。
-
求线性方程组
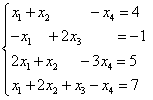 的通解。(要求用它的一个特解和导出组的基础解系表示)
的通解。(要求用它的一个特解和导出组的基础解系表示) -
已知矩阵
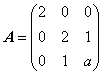 的一个特征值为1,求数a,并求正交矩阵Q和对角矩阵Λ,使得Q-1AQ =Λ。
的一个特征值为1,求数a,并求正交矩阵Q和对角矩阵Λ,使得Q-1AQ =Λ。 -
求向量组α1=(1,2,1,-1)T,α2=(0,1,2,-1)T,α3=(1,3,3,-2)T,α4=(2,1,-4,1)T,α5=(-1,-4,-5,3)的秩和一个极大线性无关组,并将向量组中的其余向量由该极大线性无关组线性表出。
-
将可逆矩阵
 表示为初等矩阵的乘积。
表示为初等矩阵的乘积。 -
计算行列式
 的值。
的值。 -
设矩阵
 ,矩阵X满足XA=B,求X。
,矩阵X满足XA=B,求X。 -
设A为2阶矩阵,若矩阵2E-A,3E-A均不可逆,则|A|=______。
-
设3阶矩阵A的秩为2,α1, α2为非齐次线性方程组Ax=b的两个不同解,则方程组Ax=b的通解为______。
相关试卷
2005年初级经济师考试《旅游经济专
所属类型:真题考试2021-03-22
初级旅游经济师试题及答案一
所属类型:模拟考试2021-03-22
初级旅游经济师试题及答案二
所属类型:模拟考试2021-03-22
2005年初级经济师考试《邮电经济专
所属类型:真题考试2021-03-22
初级经济师试题及答案1(邮电经济)
所属类型:模拟考试2021-03-22
初级经济师试题及答案1(保险经济)
所属类型:模拟考试2021-03-22
初级经济师试题及答案2(邮电经济)
所属类型:模拟考试2021-03-22
初级经济师试题及答案2(保险经济)
所属类型:模拟考试2021-03-22
初级经济师试题及答案3(保险经济)
所属类型:模拟考试2021-03-22
2014年经济师初级考试真题《建筑经
所属类型:真题考试2021-03-22
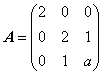 的一个特征值为1,求数a,并求正交矩阵Q和对角矩阵Λ,使得Q-1AQ =Λ。
的一个特征值为1,求数a,并求正交矩阵Q和对角矩阵Λ,使得Q-1AQ =Λ。 表示为初等矩阵的乘积。
表示为初等矩阵的乘积。 的值。
的值。 ,矩阵X满足XA=B,求X。
,矩阵X满足XA=B,求X。