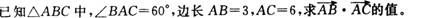某人打靶，每枪命中目标的概率都是0．9，则4枪中恰有2枪命中目标的概率为（）。

请以“函数的单调性”为课题，完成下列教学设计。（1）教学目标；（2）教学重点、难点；（3）教学过程（只要求写出新课导人和新知探究、巩固和应用）。

在《数学课程标准》的“课程实施建议”中，有这样一段叙述：在初中学段中，……评价时应将书面考试与其他评价方式有机结合。在采用书面考试时，要按照《标准》要求，避免偏题、怪题和死记硬背的题目；要设计结合现实情景的问题，……要控制客观题型的比例，设置一些探索题与开放题。请根据以上叙述，回答以下问题：（1）“其他评价方式”指的是哪些方式?（至少写出四个）（2）“设计结合现实情景的问题”是用来考查学生的何种能力?（3）“设置一些探索题与开放题”有何意义?

以下是某应用教学课堂的情境：某股民在上星期五以每股27元的价格买进某股票1000股。该股票的涨跌情况如下表（单位：元）。

师：星期四收盘时，每股多少元?生：（疑惑不解状）。提问生：27－2．5=25．5（元）。师：星期四收盘价实际上就是求有理数的和，应该为32元。师：周二收盘价最高为35．5元；周五最低为26元。师：已知该股民买进股票时付出了3‰的交易税，卖出股票时需付成效额3‰的手续费和2‰的交易税，如果该股民在星期五收盘前将全部股票卖出，他的收益情况如何?提问生（困惑状）：买入：27×1000×（1+3‰）=27081（元）；卖出：26 × 1000×（1+3‰+2‰）=26130（元）；收益：26130－27081=－951（元）。师：对不对呢?买入股票所花费的资金总额为：27×1000 ×（1+3‰）=27081（元）；卖出股票时所得资金总额为：26×1000×（1－3‰－2‰）=25870（元）；上周交易的收益为：25870－27081=－1211（元），实际亏损了1211元。师：明白了吗?请听明白的同学举手。此时课堂上约有三、四个学生举起了手，绝大部分学生眼中闪烁着疑惑之意。有些学生在窃窃私语，……少部分学生烦躁之意露于言袁。问题：（1）请指出教学中的不足之处。（2）该案例对你有什么启发?

设f（x）是连续函数，

教师的教学语言有哪些要求?

数形结合思想是一种重要的数学思想，它的实质就是根据数与形之间的对应关系，通过数与形的相互转化来解决问题。用数形结合思想解题能简化推理和运算，具有直观、快捷的优点。请简要谈谈数形结合思想在解哪些类型的问题时可以发挥作用，使问题得到更好的解决。

在一次抗洪抢险中，准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐。已知只有5

(1)求油罐被引爆的概率；

(2)如果引爆或子弹打光则停止射击，设射击次数为ξ，求ξ的分布列及ξ的数学期望。

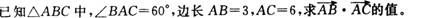
简述初中数学新课程的教学内容体系。

某人打靶，每枪命中目标的概率都是0．9，则4枪中恰有2枪命中目标的概率为（）。